Skillnad mellan versioner av "3.3 Ekvationer 2 kolumner"

Från Mathonline
Hoppa till: navigering, sök
m
m
Rad 199: Rad 199:
 
<table>
 
<table>
 
<tr>
 
<tr>
−
   <td>==== <b><span style="color:#931136">Begreppsförklaringar</span></b> ====
+
   <td>
 +
==== <b><span style="color:#931136">Begreppsförklaringar</span></b> ====
  
 
<b><span style="color:red">Variabler</span></b> är platshållare för tal och betecknas med
 
<b><span style="color:red">Variabler</span></b> är platshållare för tal och betecknas med

Versionen från 12 januari 2017 kl. 15.01

       Genomgång          Quiz          Övningar          Lathund      


Vad är en ekvation? \( \qquad\qquad\qquad\qquad\qquad\qquad\;\; \) Varför ekvationer?

\( \qquad \)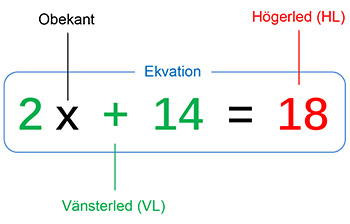Ekvation Obekant VL HL 350.jpg


En ekvation är en likhet mellan två uttryck,

har alltid formen VL = HL och innehåller

endast EN variabel, kallad obekant, se

exemplet ovan.

Ekvationens lösning: \( \quad\; \)
\( x \; = \; {\color{Red} 2} \)

Kontroll:     Sätt in lösningen i ekvationen.

  VL \( \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 \)

  HL \( \, = \, 18 \)

  VL \( \; = \; \) HL \( \qquad \Longrightarrow \qquad \) OK

  Dvs lösningen \( \, x = {\color{Red} 2} \, \) är korrekt.

Kontroll kallas ibland även för prövning.

\( \qquad\qquad \)

Exempel på en textuppgift:

Kalle köper en flaska dryck som kostar \( \, 18 \, \) kr med pant.
Drycken (innehållet) kostar \( \, 14 \, \) kr mer än panten (flaskan).
Hur mycket kostar flaskan?

Försök att lösa uppgiften utan ekvation.

Lösning med ekvation: \( \quad\;\;\; x \; = \; {\rm flaskans\;pris} \)

\[ \quad\;\; x \, + \, 14 \; = \; {\rm dryckens\;pris} \]
\[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad & \\ 2\,x \, & = & 4 & \qquad & \\ x \, & = & {\color{Red} 2} & & \end{array}\]


Svar:     Flaskan kostar \( \, {\color{Red} {2 \; {\rm kr\,}}}\). \( \;\; \) Utan ekvation svarar de flesta fel (4 kr).


För mer info om lösningsmetoder och om hur man ställer upp ekvationen, se:


\( \qquad\; \)Övertäckningsmetoden \( \quad \) och \( \quad \) Allmän metod.



Ekvationslösning: Övertäckningsmetoden


Exemplet ovan:

  \( 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x \)

\(\quad\)
\( \, + \;\, 14 \; = \; 18 \)

  \( \;\, {\color{Red} ?} \;\;\; + \; 14 \; = \; 18 \)

  \( \;\, {\color{Red} 4} \;\;\; + \; 14 \; = \; 18 \)

  \( \;\, \Downarrow \)

  \( \, 2 \, \cdot \; x \;\; = \;\, {\color{Red} 4} \qquad\quad {\color{Red} {\rm Täck\;över\;}} x \)

  \( \, 2 \, \cdot \; \)
\( \quad \)
\( \; = \;\, 4 \)

  \( \, 2 \, \cdot \; {\color{Red} ?} \;\; = \;\; 4 \)

  \( \, 2 \, \cdot \; {\color{Red} 2} \;\; = \;\; 4 \)

  \( \quad\;\;\; \Downarrow \)

 
\( \; x \; = \; {\color{Red} 2} \)


Ekvationslösning: Allmän metod


Exemplet ovan:

\[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad | & {\color{Red} {- \, 14}} \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ 2 \cdot x \, & = & 4 & \qquad | & {\color{Red} {/ \; 2}} \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x \, & = & 2 & & \end{array}\]

Skrivsättet \( \quad\;\;\, | \quad {\color{Red} {- \, 14}} \quad\;\;\, \) är en kommentar och betyder:

Subtrahera \( \, 14 \, \) från ekvationens båda led.

Kommentaren \( \;\; | \quad {\color{Red} {/ \; 2}} \;\; \) betyder:

Dividera ekvationens båda led med \( \, 2 \).


Ekvation som en våg i balans


Målet: \( \qquad\quad \) Att isolera \( \, {\color{Red} x} \, \) på ett led.


Steg 1:

  Förenkla uttrycken i ekvationens båda led så långt som

  möjligt: Se raderna 1-3 i exemplet ovan (VL).


Steg 2:

  Utför samma operation på ekvationens båda led med

  målet att isolera \( \, x \, \): Se raderna 3 och 5 i exemplet ovan.

  Förenkla de nyuppkomna uttrycken.


Regel:    Vilken operation?    Den som isolerar \( \, x \, \).

  Rad 3 i exemplet ovan:

\[ 2\,x \, + \, 14 \; = \; 18 \qquad\quad | \;\; {\color{Red} {- \, 14}} \]

 \( \, {\color{Red} {- \, 14}} \, \) är den inversa (motsatta) operationen till \( \, + \, 14 \, \).

  Rad 5 i exemplet ovan:

\[ \;\; 2 \cdot x \; = \; 4 \]

  Eller: \( \qquad\quad\;\, x \cdot 2 \; = \; 4 \qquad\quad\;\;\, | \;\; {\color{Red} {/ \; 2}} \)

  \( \, {\color{Red} {/ \; 2}} \, \) är den inversa operationen till \( \, \cdot \; 2 \, \).



Begreppsförklaringar


Begreppsförklaringar

Variabler är platshållare för tal och betecknas med

bokstäver, jämförbart med lådor som har etiketter.

Innehållet är variabelns värde (tal) och kan bytas ut.

Obekant är en variabel som förekommer i en ekvation.

Uttryck är en kombination av variabler, tal, räkneopera-

tioner och parenteser som till slut, när uttrycket beräk-

nas, ger ett värde: uttryckets värde, se 3.1 Uttryck.

    
God redovisningsstil vid ekvationslösning:
  • Definiera vad din obekant står för.
  • Skriv likhetstecknen exakt under varandra (samma kolumn).
  • Kommentera, när det behövs, det du gör antingen genom att   
använda skrivsättet i exemplet ovan eller på ditt eget sätt,
bara det blir förståeligt vad du gör.
  • Skriv kommentarerna skilda från ekvationens lösningsgång.

Ekvation är en likhet mellan två uttryck med endast EN obekant (än så länge i Matte 1).

Formel är en likhet mellan två uttryck med minst två variabler, behandlas i 3.8 Formler.




Copyright © 2010-2016 Math Online Sweden AB. All Rights Reserved.

Hämtad från "https://matte1b.mathonline.se/index.php?title=3.3_Ekvationer_2_kolumner&oldid=31454"