Skillnad mellan versioner av "3.3 Ekvationer+"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 163: | Rad 163: | ||
<math> \;\;\; </math> <b><span style="color:red">Samma operation på båda leden !</span></b> | <math> \;\;\; </math> <b><span style="color:red">Samma operation på båda leden !</span></b> | ||
</big></div> | </big></div> | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">När saknar en ekvation lösning?</span></b> == | ||
| + | |||
| + | <br> | ||
| + | |||
| + | <div class="ovnC"> | ||
| + | <big><b><span style="color:#931136">Exempel:</span></b></big> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | ::<math>\begin{array}{rclcl} x \, - \, (x \, + \, 4) & = & 8 & & \\ | ||
| + | x \, - \, x \, - \, 4 & = & 8 & & \\ | ||
| + | 2\,x \, + \, 14 & = & 18 & & \\ | ||
| + | 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ | ||
| + | 2 \cdot x \, & = & 4 & & \\ | ||
| + | \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ | ||
| + | x \, & = & 2 & & | ||
| + | \end{array}</math> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | </div> | ||
Versionen från 2 augusti 2017 kl. 15.08
| Genomgång Ekvationer | Quiz | Övningar Webb | Lathund | Nästa avsnitt >> |
| << Förra avsnitt | Övningar App |
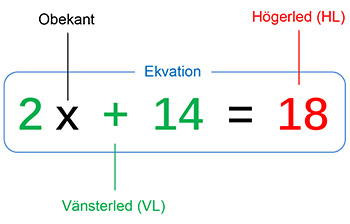
Vad är en ekvation?
En ekvation är en likhet mellan två uttryck,
har alltid formen VL = HL och innehåller
endast EN variabel, kallad obekant.
Ex.: \( \qquad\quad 2\,x \; + \; 14 \; = \; 18 \)
Ekvationens lösning: \( \quad\; \)
- Varför?
Kontroll: Sätt in lösningen i ekvationen.
VL \( \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 \)
HL \( \, = \, 18 \)
VL \( = \) HL \( \, \Rightarrow \, x = {\color{Red} 2} \) är en korrekt lösning.
Kontroll kallas ibland även för prövning.
Två lösningsmetoder:
1. Övertäckningsmetoden
Exemplet ovan:
\( 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x \)
\( \;\, {\color{Red} ?} \;\;\; + \; 14 \; = \; 18 \)
\( \;\, {\color{Red} 4} \;\;\; + \; 14 \; = \; 18 \)
\( \;\, \Downarrow \)
\( \, 2 \, \cdot \; x \;\; = \;\, {\color{Red} 4} \qquad\quad {\color{Red} {\rm Täck\;över\;}} x \)
\( \, 2 \, \cdot \; \)\( \, 2 \, \cdot \; {\color{Red} ?} \;\; = \;\; 4 \)
\( \, 2 \, \cdot \; {\color{Red} 2} \;\; = \;\; 4 \)
\( \quad\;\;\; \Downarrow \)
2. Allmän metod
Steg 1
Förenkla uttrycken i ekvationens båda led
så långt som möjligt. I exemplet ovan:
- \[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & & \end{array}\]
Steg 2
Utför samma operation på båda leden:
- \[\begin{array}{rcl} 2\,x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} \\ 2\,x \, & = & 4 \end{array}\]
Vilken operation?
Den inversa operation som isolerar \( x\)-termen.
\( \;\;\; {\color{Red} {- \, 14}} \, \) är den inversa operationen till \( \, + \, 14 \)
Steg 3
Utför samma operation på båda leden:
- \[\begin{array}{rclcl} \quad\; 2 \cdot x \, & = & 4 & & \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x & = & 2 & & \end{array}\]
Vilken operation?
Den inversa operation som isolerar \( \, x \, \).
\( \quad\;\; {\color{Red} {/ \; 2}} \, \) är den inversa operationen till \( \, \cdot \; 2 \)
Ekvationslösningens filosofi:
Betrakta ekvationen som en våg i balans.
Likhetstecknet \( \; = \; \) Vågens balans
HL och VL\( \; = \; \) Vågens skålar
Bibehåll balansen genom att göra samma
sak på båda vågskålarna, dvs:
\( \;\;\; \) Samma operation på båda leden !
När saknar en ekvation lösning?
Exempel:
- \[\begin{array}{rclcl} x \, - \, (x \, + \, 4) & = & 8 & & \\ x \, - \, x \, - \, 4 & = & 8 & & \\ 2\,x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ 2 \cdot x \, & = & 4 & & \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x \, & = & 2 & & \end{array}\]
Copyright © 2010-2017 Math Online Sweden AB. All Rights Reserved.