Skillnad mellan versioner av "1.7 Lathund till Potenser Webbversion"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(64 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 +
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
Rad 5: Rad 6:
 
{{Not selected tab|[[1.7 Quiz till Potenser|Quiz]]}}
 
{{Not selected tab|[[1.7 Quiz till Potenser|Quiz]]}}
 
{{Not selected tab|[[1.7 Övningar till Potenser|Övningar]]}}
 
{{Not selected tab|[[1.7 Övningar till Potenser|Övningar]]}}
−
{{Selected tab|[[1.7 Formelsamling till Potenser|Formelsamling Potenser]]}}
+
{{Selected tab|[[1.7 Lathund till Potenser Webbversion|Lathund Webb]]}}
 +
| style="border-bottom:1px solid #797979"  width="100%"|  
 +
|}
 +
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 +
| style="border-bottom:1px solid #797979" width="5px" |  
 +
{{Not selected tab|    }}
 +
{{Not selected tab|    }}
 +
{{Not selected tab|    }}
 +
{{Not selected tab|    }}
 +
{{Not selected tab|[[1.7 Lathund till Potenser Appversion|Lathund App]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"|  
 
| style="border-bottom:1px solid #797979"  width="100%"|  
 
|}
 
|}
  
−
__NOTOC__  <!-- __TOC__ -->
 
−
== <b><span style="color:#931136">Vad är en potens?</span></b> ==
 
  
 +
== <b><span style="color:#931136">Potens</span></b> ==
 +
<br />
 
<table>
 
<table>
 
<tr>
 
<tr>
−
   <td><div class="border-divblue">
+
   <td>[[Image: Potens Bas Exponent_80.jpg]]</td>
−
<b>Potens:</b>
+
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<div class="ovnE">
 +
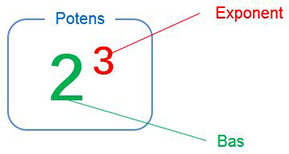
<big>Potens med positiv exponent<span style="color:black">:</span>
  
−
::<math> 2\,^{\color{Red} 3} \; = \;\; \underbrace{2 \, \cdot \, 2 \, \cdot \, 2}_{{\color{Red} 3}\;\times} </math>  
+
<math> \quad\;\;\; 2\,^{\color{Red} 3} \; = \;\; \underbrace{2 \, \cdot \, 2 \, \cdot \, 2}_{{\color{Red} 3}\;\times} \; = \; 8</math>  
  
−
<b>Upprepad multiplikation av </b>
+
<b><span style="color:#931136">Potens</span></b> = upprepad <b><span style="color:red">multiplikation</span></b>
  
−
<b><math>2 \, </math> med sig själv, <math> \, {\color{Red} 3} \, </math> gånger.</b>  
+
av <math> \, 2 \, </math> med sig själv, <math> \, {\color{Red} 3} \, </math> gånger.  
−
</div>
+
</big></div>
 
</td>
 
</td>
−
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Potens Bas Exponent_80.jpg]]</td>
 
 
</tr>
 
</tr>
 
</table>
 
</table>
 +
<br />
 +
<table>
 +
<tr>
 +
  <td><div class="ovnA">
 +
<big>Potens med exponenten <math> \, {\color{Red} 0} \, </math><span style="color:black">:</span>
  
 +
<math> \qquad\quad \displaystyle 2\,^{\color{Red} 0} \;\; = \;\; 1 </math>
 +
</big></div>
  
−
== <b><span style="color:#931136">Potenslagarna</span></b> ==
 
−
<div class="tolv"> <!-- tolv3 -->
 
  
−
Följande lagar gäller för potenser där basen <math> a\, </math> är ett tal <math> \neq 0 </math>, exponenterna <math> \, x \, </math> och <math> \, y \, </math> godtyckliga tal och <math> m,\,n </math> heltal (<math> n\neq 0 </math>):
 
−
</div> <!-- tolv3 -->
 
  
  
−
<div class="border-divblue">
 
−
<b><span style="color:#931136">Första potenslagen:</span></b> <big><math> \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad </math></big>
 
−
----
 
−
<b><span style="color:#931136">Andra potenslagen:</span></b> <big><math> \qquad\qquad\qquad\quad \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad </math></big>
 
−
----
 
−
<b><span style="color:#931136">Tredje potenslagen:</span></b> <big><math> \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad </math></big>
 
−
----
 
−
<b><span style="color:#931136">Lagen om nollte potens:</span></b> <big><math> \qquad\qquad\qquad\! a\,^0 \; = \; 1 \qquad\qquad </math></big>
 
−
----
 
−
<b><span style="color:#931136">Lagen om negativ exponent:</span></b> <big><math> \qquad\qquad a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad </math></big>
 
−
----
 
−
<b><span style="color:#931136">Potens av en produkt:</span></b> <big><math> \qquad\qquad\;\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad </math></big>
 
−
----
 
−
<b><span style="color:#931136">Potens av en kvot:</span></b> <big><math> \qquad\qquad\qquad \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad </math></big>
 
−
</div> <!-- border-divblue -->
 
  
  
−
<div class="tolv"> <!-- tolv3a -->
 
−
För enkelhets skull definierades potensbegreppet inledningsvis endast för positiva heltalsexponenter <math> \, x \, </math> och <math> \, y </math>. Men potenslagarna gäller även för exponenter som är negativa eller bråktal. I formuleringen "negativ exponent" antas <math> \, x > 0 </math>.
 
−
</div> <!-- tolv3a -->
 
  
  
−
<div class="exempel"> <!-- exempel3 -->
 
−
== <b><span style="color:#931136">Exempel 3</span></b> ==
 
−
<big>
 
  
−
::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; {a \cdot a \cdot a \cdot a \cdot a \; \over \; a \cdot a \cdot a} \; = \; {a \cdot a \cdot \cancel{a \cdot a \cdot a} \; \over \; \cancel{a \cdot a \cdot a}} \; = \; a \cdot a \; = \; a\,^2 </math></big>
 
  
−
Snabbare med andra potenslagen:
 
  
−
::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5\,-\,3}}} \; = \; a\,^2 </math></big>
 
−
</big>
 
−
</div> <!-- exempel3 -->
 
  
 +
</td>
 +
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<div class="ovnC">
 +
<big>Potens med negativ exponent<span style="color:black">:</span>
  
−
<div class="tolv"> <!-- tolv2 -->
+
<math> \qquad \displaystyle 2\,^{\color{Red} {-3}} \; = \;\; \frac{1}{2\,^{\color{Red} {3}}} \; = \; \frac{1}{8} \quad </math>  
−
'''Påstående (Lagen om nollte potens)''':
+
  
−
::::<big><math> a^0 \; = \; 1 </math></big>
+
<b><span style="color:red">Invertera</span></b> potensen med positiv <math> \quad </math>
  
−
'''Bevis''':
+
exponent.
  
−
Påståendet kan bevisas genom att använda andra potenslagen:
+
----
  
−
::::<big><math> \displaystyle{a^x \over a^x} \; = \; a^{x-x} \; = \; a^0 </math></big>
+
Att <b><span style="color:red">"invertera"</span></b> t.ex. <math> \, 10 \, </math> ger <math> \, \displaystyle {1 \over 10} \; </math>.
 +
</big></div>
 +
</td>
 +
</tr>
 +
</table>
  
−
Å andra sidan vet vi att ett bråk med samma täljare som nämnare har värdet <math> \, 1 </math>:
 
  
−
::::<big><math> \displaystyle{a^x \over a^x} \; = \; 1 </math></big>
+
== <b><span style="color:#931136">Potenslagarna</span></b> ==
 +
<br />
 +
<div class="border-divblue">
 +
<b><span style="color:#931136">Första potenslagen:</span></b> <big><math> \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad </math></big>
 +
----
 +
<b><span style="color:#931136">Andra potenslagen:</span></b> <big><math> \qquad\qquad\qquad\;\;\; \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad </math></big>
 +
----
 +
<b><span style="color:#931136">Tredje potenslagen:</span></b> <big><math> \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad </math></big>
 +
----
 +
<b><span style="color:#931136">Lagen om nollte potens:</span></b> <big><math> \qquad\qquad\quad\;\;\, a\,^0 \; = \; 1 \qquad\qquad </math></big>
 +
----
 +
<b><span style="color:#931136">Lagen om negativ exponent:</span></b> <big><math> \qquad\quad\;\;\; a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad </math></big>
 +
----
 +
<b><span style="color:#931136">Potens av en produkt:</span></b> <big><math> \qquad\qquad\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad </math></big>
 +
----
 +
<b><span style="color:#931136">Potens av en kvot:</span></b> <big><math> \qquad\qquad\qquad\, \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad </math></big>
 +
</div> <!-- border-divblue -->
  
−
Av raderna ovan följer påståendet:
 
  
−
::::<big><math> a^0 \; = \; 1 </math></big>
+
== <b><span style="color:#931136">Grundpotensform</span></b> ==
−
</div> <!-- tolv4 -->
+
<br />
 +
::[[Image: Grundpotensform_60b.jpg]]
  
  
−
<div class="exempel"> <!-- exempel4 -->
+
<div class="border-divblue">
−
== <b><span style="color:#931136">Exempel på potenser med negativa exponenter</span></b> ==
+
== <small><b><span style="color:#931136">Definition:</span></b></small> ==
−
<big>
+
  
−
::::<math> \displaystyle{10\,^{-1} \, = \, {1 \over 10\,^1} \, = \, {1 \over 10} \, = \, 0,1} </math>
 
−
 
−
::::<math> \displaystyle{10\,^{-2} \, = \, {1 \over 10\,^2} \, = \, {1 \over 10 \cdot 10} \, = \, {1 \over 100} \, = \, 0,01} </math>
 
−
 
−
::::<math> \displaystyle{10\,^{-3} \, = \, {1 \over 10\,^3} \, = \, {1 \over 10 \cdot 10 \cdot 10} \, = \, {1 \over 1000} \, = \, 0,001} </math>
 
−
</big>
 
−
</div> <!-- exempel4 -->
 
−
 
−
 
−
<div class="tolv"> <!-- tolv4a -->
 
−
 
−
'''Påstående (Lagen om negativ exponent, <math> \, x > 0 </math>)''':
 
−
 
−
::::<big><math> a^{-x} = \displaystyle{1 \over a^x} </math></big>
 
−
 
−
'''Bevis''':
 
−
 
−
Påståendet kan bevisas genom att använda lagen om nollte potensen (baklänges) samt andra potenslagen:
 
−
 
−
::::<big><math> \displaystyle{1 \over a^x} \; = \; \displaystyle{a^0 \over a^x} \; = \; a^{0-x} \; = \; a^{-x} </math></big>
 
−
 
−
Vi får påståendet, fast baklänges.
 
−
</div> <!-- tolv4a -->
 
−
 
−
 
−
<div class="tolv"> <!-- tolv5 -->
 
−
Att potenser med negativa exponenter är en naturlig fortsättning på potenser med positiva exponenter med nollte potensen däremellan illustrerar följande exempel:
 
−
</div> <!-- tolv5 -->
 
−
 
−
 
−
<div class="exempel"> <!-- exempel4 -->
 
−
== <b><span style="color:#931136">Varför är <math> \; 5\,^0 \, = \, 1 \; </math>?</span></b> ==
 
 
<big>
 
<big>
 +
<b><span style="color:#931136"><math> a \cdot 10\,^n \; </math></span></b> kallas <b><span style="color:#931136">grundpotensform</span></b> om <b><span style="color:#931136"><math> n \, </math></span></b> är heltal och <math> \; 1 \leq </math> <b><span style="color:#931136"><math> a </math></span></b> <math> < 10 \; </math>.
  
−
::::<math> \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 </math>
+
Dvs <b><span style="color:#931136"><math> \, a \, </math></span></b> måste vara mellan <math> \, 1,\ldots \, </math> och <math> \, 9,\ldots \; </math>.</big>
−
 
+
</div>
−
::::<math> \;\; 5^3 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 </math>
+
−
 
+
−
::::<math> \;\; 5^2 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 </math>
+
−
 
+
−
::::<math> \;\; 5^1 \; = \; {\color{Red} 1} \cdot 5 </math>
+
−
 
+
−
::::<math> \;\; {\color{Red} {5^0 \; = \; 1}} </math>
+
−
 
+
−
::::<math> \;\; 5^{-1} \; = \; \displaystyle{{\color{Red} 1} \over 5} </math>
+
−
 
+
−
::::<math> \;\; 5^{-2} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5} </math>
+
−
 
+
−
::::<math> \;\; 5^{-3} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5} </math>
+
−
 
+
−
::::<math> \;\; 5^{-4} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5 \cdot 5 } </math>
+
−
 
+
−
Att <math> \; {\color{Red} 1} </math>-orna följer med hela tiden beror på att multiplikationens ''enhet'' är <math> \, {\color{Red} 1} </math>, dvs <math> \, a \cdot {\color{Red} 1} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 1} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5^0}} \, </math> då alla <math> \, 5</math>-or har försvunnit.
+
−
</big>
+
−
</div> <!-- exempel4 -->
+
−
 
+
−
 
+
−
<div class="tolv"> <!-- tolv5 -->
+
−
Jämför med:
+
−
</div> <!-- tolv5 -->
+
−
 
+
−
 
+
−
<div class="exempel"> <!-- exempel5 -->
+
−
== <b><span style="color:#931136">Varför är <math> \; 5 \cdot 0 \, = \, 0 \; </math>?</span></b> ==
+
−
<big>
+
−
 
+
−
::::<math> \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot 3 \; = \; {\color{Red} 0} + 5 + 5 + 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot 2 \; = \; {\color{Red} 0} + 5 + 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot 1 \; = \; {\color{Red} 0} + 5 </math>
+
−
 
+
−
::::<math> \;\; {\color{Red} {5 \cdot 0 \; = \; 0}} </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot (-1) \; = \; {\color{Red} 0} - 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot (-2) \; = \; {\color{Red} 0} - 5 - 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot (-3) \; = \; {\color{Red} 0} - 5 - 5 - 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot (-4) \; = \; {\color{Red} 0} - 5 - 5 - 5 - 5 </math>
+
−
 
+
−
Att <math> \; {\color{Red} 0} </math>-orna följer med hela tiden beror på att additionens ''enhet'' är <math> \, {\color{Red} 0} </math>, dvs <math> \, a + {\color{Red} 0} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 0} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5 \cdot 0}} \, </math> då alla <math> \, 5</math>-or har försvunnit.
+
−
</big>
+
−
</div> <!-- exempel5 -->
+
  
  
Rad 191: Rad 116:
  
  
−
[[Matte:Copyrights|Copyright]] © 2010-2015 Math Online Sweden AB. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2019 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 26 september 2019 kl. 11.15

       Genomgång Potenser          Genomgång Grundpotensform          Quiz          Övningar          Lathund Webb      
                                               Lathund App      


Potens


Potens Bas Exponent 80.jpg            

Potens med positiv exponent:

\( \quad\;\;\; 2\,^{\color{Red} 3} \; = \;\; \underbrace{2 \, \cdot \, 2 \, \cdot \, 2}_{{\color{Red} 3}\;\times} \; = \; 8\)

Potens = upprepad multiplikation

av \( \, 2 \, \) med sig själv, \( \, {\color{Red} 3} \, \) gånger.


Potens med exponenten \( \, {\color{Red} 0} \, \):

\( \qquad\quad \displaystyle 2\,^{\color{Red} 0} \;\; = \;\; 1 \)







           

Potens med negativ exponent:

\( \qquad \displaystyle 2\,^{\color{Red} {-3}} \; = \;\; \frac{1}{2\,^{\color{Red} {3}}} \; = \; \frac{1}{8} \quad \)

Invertera potensen med positiv \( \quad \)

exponent.

Att "invertera" t.ex. \( \, 10 \, \) ger \( \, \displaystyle {1 \over 10} \; \).


Potenslagarna


Första potenslagen: \( \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad \)

Andra potenslagen: \( \qquad\qquad\qquad\;\;\; \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad \)

Tredje potenslagen: \( \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad \)

Lagen om nollte potens: \( \qquad\qquad\quad\;\;\, a\,^0 \; = \; 1 \qquad\qquad \)

Lagen om negativ exponent: \( \qquad\quad\;\;\; a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad \)

Potens av en produkt: \( \qquad\qquad\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad \)

Potens av en kvot: \( \qquad\qquad\qquad\, \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad \)


Grundpotensform


Grundpotensform 60b.jpg


Definition:

\( a \cdot 10\,^n \; \) kallas grundpotensform om \( n \, \) är heltal och \( \; 1 \leq \) \( a \) \( < 10 \; \).

Dvs \( \, a \, \) måste vara mellan \( \, 1,\ldots \, \) och \( \, 9,\ldots \; \).





Copyright © 2019 TechPages AB. All Rights Reserved.

Hämtad från "https://matte1b.mathonline.se/index.php?title=1.7_Lathund_till_Potenser_Webbversion&oldid=34649"