Skillnad mellan versioner av "4.8 Beräkningar med funktioner"

Från Mathonline
Hoppa till: navigering, sök
(Skapade sidan med '__NOTOC__ {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | style="border-bottom:1px solid #797979" width="5px" |   {{Not selected tab|4.6 Expone...')
 
m
 
(83 mellanliggande versioner av samma användare visas inte)
Rad 2: Rad 2:
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[4.6 Exponentialfunktioner | <<<&nbsp;&nbsp;Förra avsnitt]]}}
+
{{Not selected tab|[[4.7 Olika matematiska modeller| <<&nbsp;&nbsp;Förra avsnitt]]}}
−
{{Not selected tab|[[4.7 Olika matematiska modeller|Genomgång]]}}
+
{{Selected tab|[[4.8 Beräkningar med funktioner|Genomgång]]}}
−
{{Selected tab|[[4.7 Övningar till Olika matematiska modeller|Övningar]]}}
+
{{Not selected tab|[[4.8 Övningar till Beräkningar med funktioner|Övningar]]}}
−
<!-- {{Not selected tab|[[4.7 Olika matematiska modeller|Nästa avsnitt&nbsp;&nbsp;>> ]]}} -->
+
{{Not selected tab|[[4.9 En funktions definitions- & värdemängd|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 +
<!-- {{Not selected tab|[[Diagnosprov i Matte 1b till kap 1 Linjära ekvationssystem & kap 2 Funktionslära|Diagnosprov&nbsp;&nbsp;>> ]]}} -->
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
−
<div class="ovnE">
+
= <b><span style="color:#931136">Exempel på funktioner</span></b> =
  
−
<big>
+
<div class="ovnE"><big>
−
<b><span style="color:#931136">&nbsp;&nbsp;&nbsp;&nbsp;Gör övningarna i boken Origo 1b:</span></b>
+
:<math> y \, = \, f(x) \, = \, 4\,x + 12 </math>
  
−
----
+
:<math> y \, = \, g(x) \, = \, 3\,x^2 + 5\,x - 16 </math>
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Sidan 199.
+
:<math> y \, = \, h(x) \, = \, 8\,x^3 - 4\,x</math>
  
−
----
+
</big></div>
  
−
<b><span style="color:#931136">&nbsp;&nbsp;&nbsp;&nbsp;I Origo 1c:</span></b>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Sidan 183.
 
  
−
----
+
= <b><span style="color:#931136">En funktions värde</span></b> =
 +
<div class="ovnC"><big>
 +
En funktion definieras med uttrycket till höger om likhetstecknet, kallat <b><span style="color:red">funktionsuttryck</span></b>. 
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Kolla dina resultat i bokens facit.
+
Därför är funktionens värde uttryckets värde. Precis som ett uttryck har en
−
</big>
+
−
</div>
+
  
 +
funktion inget värde för sig utan <b><span style="color:red">får</span></b> ett värde endast för ett visst <math>\,\color{Red}x\,</math>.
  
 +
<b><span style="color:#931136">Exempel:</span></b> &nbsp;&nbsp; Beräkna följande funktions värde för <math> \, \color{Red}{x = 0,5} \, </math>:
  
 +
::::::<math> y \, = \, h(x) \, = \, 8\,x^3 - 4\,x </math>
  
 +
<b><span style="color:#931136">Lösning:</span></b> &nbsp;&nbsp; Vi sätter in <math> 0,5\,</math> för <math>x\,</math> i funktionen och beräknar funktionsuttryckets värde:
  
 +
::::::<math> h(0,5) \, = \, 8 \cdot 0,5^3 - 4 \cdot 0,5 = 8 \cdot 0,125 - 2 = 1 - 2 = -1 \,</math>
  
 +
Den givna funktionens värde för <math> \, x = 0,5\, </math> är <math> \, -1\,</math>. Man skriver: &nbsp;&nbsp;&nbsp; <div class="smallBoxVariant"><math> h(0,5) \, = \, -1 </math></div>
  
 +
För andra värden på <math>\,x\,</math> kommer funktionen att ha andra värden.
 +
</big></div>
  
  
 +
= <b><span style="color:#931136">Uppgift Vinternatt</span></b> =
 +
<div class="ovnA"><big>
 +
<table>
 +
<tr>
 +
  <td>[[Image: Ex 1 Temp Vinternatt.jpg]]</td>
 +
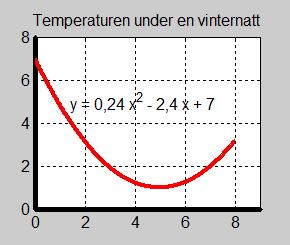
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Under en vinternatt varierar temperaturen enligt funktionen
  
 +
::::<math> y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 </math>
  
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; där &nbsp;&nbsp;&nbsp; <math> y \;\, = </math> &nbsp; temperaturen i grader Celsius och
  
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <math> x \;\, = </math> &nbsp; tiden i timmar efter midnatt
  
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; a) &nbsp; Bestäm vinternattens temperatur algebraiskt vid:
  
 +
:::::'''kl 2 &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; kl 5 &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; kl 7'''
  
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; b) &nbsp; Jämför resultaten i a) med grafen till <math> \, y = f(x) \, </math> på bilden till vänster.
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; c) &nbsp; Avläs vinternattens lägsta temperatur från grafen. När inträffar den?
 +
</td>
 +
</tr>
 +
</table>
 +
</big></div>
 +
 +
 +
= <b><span style="color:#931136">Dagens inlämningsuppgift</span></b> =
 +
 +
<div class="ovnA"><big>
 +
:Lös uppgiften Vinternatt.
 +
 +
:Skriv dina lösningar i ren form. OBS! ingen kladd.
 +
 +
:Lösningarna ska vara tydliga, läsliga och strukturerade på ett A4-blad.
 +
 +
:Att endast ange svaret godtas ej. Du ska redovisa <i>hur</i> du kommer dit.
 +
 +
:Fota A4-bladet med din mobil och ladda upp det till Schoolitys "Uppgift".
 +
 +
:Deadline för inlämning: kl 18 lektionsdagen.
 +
</big></div>
 +
 +
 +
= <b><span style="color:#931136">Dagens övningar</span></b> =
 +
<div class="ovnE"><big>
 +
&nbsp;&nbsp;&nbsp;&nbsp;Gör övningarna i boken Origo 1b:
 +
 +
----
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Sidan 180
 +
 +
----
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;I Origo 1c:&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Sidan 164
 +
 +
----
  
 +
&nbsp;&nbsp;&nbsp;&nbsp;Kolla dina resultat i bokens facit.
 +
</big></div>
  
  

Nuvarande version från 25 mars 2020 kl. 07.12

        <<  Förra avsnitt          Genomgång          Övningar          Nästa avsnitt  >>      


Exempel på funktioner

\[ y \, = \, f(x) \, = \, 4\,x + 12 \]

\[ y \, = \, g(x) \, = \, 3\,x^2 + 5\,x - 16 \]

\[ y \, = \, h(x) \, = \, 8\,x^3 - 4\,x\]


En funktions värde

En funktion definieras med uttrycket till höger om likhetstecknet, kallat funktionsuttryck.

Därför är funktionens värde uttryckets värde. Precis som ett uttryck har en

funktion inget värde för sig utan får ett värde endast för ett visst \(\,\color{Red}x\,\).

Exempel:    Beräkna följande funktions värde för \( \, \color{Red}{x = 0,5} \, \):

\[ y \, = \, h(x) \, = \, 8\,x^3 - 4\,x \]

Lösning:    Vi sätter in \( 0,5\,\) för \(x\,\) i funktionen och beräknar funktionsuttryckets värde:

\[ h(0,5) \, = \, 8 \cdot 0,5^3 - 4 \cdot 0,5 = 8 \cdot 0,125 - 2 = 1 - 2 = -1 \,\]
Den givna funktionens värde för \( \, x = 0,5\, \) är \( \, -1\,\). Man skriver:    
\( h(0,5) \, = \, -1 \)

För andra värden på \(\,x\,\) kommer funktionen att ha andra värden.


Uppgift Vinternatt

Ex 1 Temp Vinternatt.jpg        Under en vinternatt varierar temperaturen enligt funktionen
\[ y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 \]

       där     \( y \;\, = \)   temperaturen i grader Celsius och

                 \( x \;\, = \)   tiden i timmar efter midnatt

       a)   Bestäm vinternattens temperatur algebraiskt vid:

kl 2                 kl 5                 kl 7

       b)   Jämför resultaten i a) med grafen till \( \, y = f(x) \, \) på bilden till vänster.

       c)   Avläs vinternattens lägsta temperatur från grafen. När inträffar den?


Dagens inlämningsuppgift

Lös uppgiften Vinternatt.
Skriv dina lösningar i ren form. OBS! ingen kladd.
Lösningarna ska vara tydliga, läsliga och strukturerade på ett A4-blad.
Att endast ange svaret godtas ej. Du ska redovisa hur du kommer dit.
Fota A4-bladet med din mobil och ladda upp det till Schoolitys "Uppgift".
Deadline för inlämning: kl 18 lektionsdagen.


Dagens övningar

    Gör övningarna i boken Origo 1b:

                    Sidan 180

    I Origo 1c:        Sidan 164

    Kolla dina resultat i bokens facit.





Copyright © 2020 TechPages AB. All Rights Reserved.

Hämtad från "https://matte1b.mathonline.se/index.php?title=4.8_Beräkningar_med_funktioner&oldid=36019"