Skillnad mellan versioner av "5.7 Problemlösning: Cirkel-kvadrat problemet"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 25: | Rad 25: | ||
<span style="color:blue">Sambandet</span> ovan är en <b><span style="color:#931136">funktion</span></b><span style="color:black">:</span> <math> \qquad </math> <div class="smallBoxVariant"><math> \displaystyle a \, = \, f(r) \, = \, \frac{\pi}{2} \cdot \, r </math></div> | <span style="color:blue">Sambandet</span> ovan är en <b><span style="color:#931136">funktion</span></b><span style="color:black">:</span> <math> \qquad </math> <div class="smallBoxVariant"><math> \displaystyle a \, = \, f(r) \, = \, \frac{\pi}{2} \cdot \, r </math></div> | ||
| − | | + | Dvs ett värde på <math> \, r \, </math> bestämmer även ett värde på <math> \, a \, </math>. |
| + | |||
| + | <math> \, r \, </math> är funktionens oberoende och <math> \, a \, </math> funktionens beroende variabel. | ||
</big> | </big> | ||
</div> | </div> | ||
Versionen från 25 mars 2020 kl. 15.11
| <<< Förra avsnitt | Genomgång | Övningar | Det duala problemet |
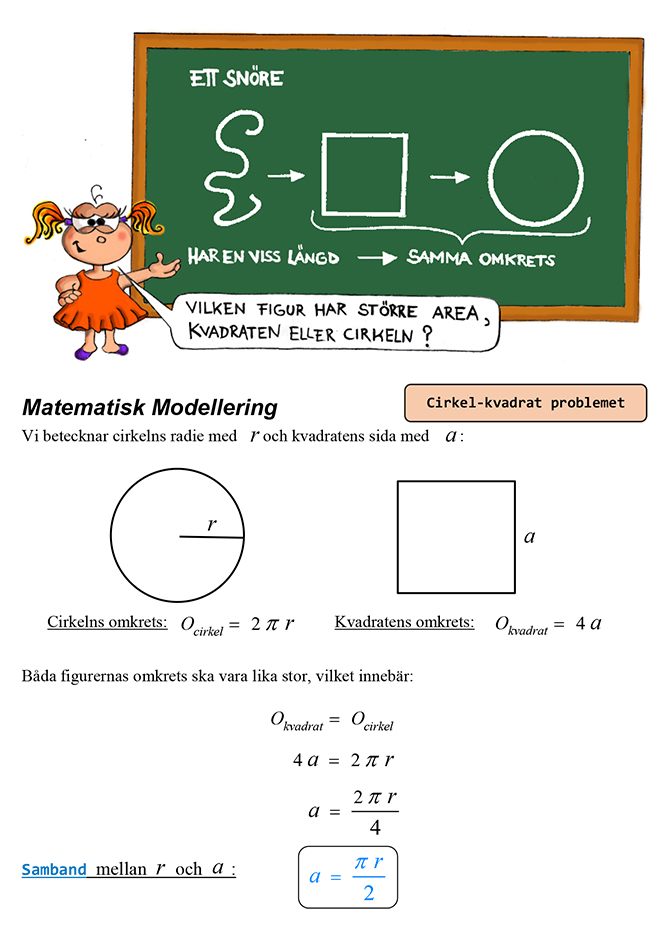
Vilken figur har större area?
Slutsats
Ska cirkeln och kvadraten ha samma omkrets måste sambandet ovan gälla.
Sambandet ovan är en funktion: \( \qquad \)\( \displaystyle a \, = \, f(r) \, = \, \frac{\pi}{2} \cdot \, r \)
Dvs ett värde på \( \, r \, \) bestämmer även ett värde på \( \, a \, \).
\( \, r \, \) är funktionens oberoende och \( \, a \, \) funktionens beroende variabel.
Dagens inlämningsuppgift
- Lös uppgiften Vinternatt.
- Skriv dina lösningar i ren form. OBS! ingen kladd.
- Lösningarna ska vara tydliga, läsliga och strukturerade på ett A4-blad.
- Att endast ange svaret godtas ej. Du ska redovisa hur du kommer dit.
- Fota A4-bladet med din mobil och ladda upp det till Schoolitys "Uppgift".
- Deadline för inlämning: kl 18 lektionsdagen.
Dagens övningar
Gör övningarna i boken Origo 1b:
Sidan 180
I Origo 1c: Sidan 164
Kolla dina resultat i bokens facit.
Copyright © 2020 TechPages AB. All Rights Reserved.