Skillnad mellan versioner av "1.3 Tal i decimalform"

Från Mathonline
Hoppa till: navigering, sök
m (→‎Periodisk decimalutveckling)
m
 
(204 mellanliggande versioner av samma användare visas inte)
Rad 2: Rad 2:
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[1.3 Decimaltal|Genomgång Decimaltal]]}}
+
{{Selected tab|[[1.3 Tal i decimalform|Genomgång]]}}
 +
{{Not selected tab|[[1.3 Quiz i decimaltal|Quiz]]}}
 +
{{Not selected tab|[[1.3 Övningar i decimaltal|Övningar]]}}
 +
<!-- {{Not selected tab|[[1.3 Decimaltal+|Genomgång+]]}} -->
 
{{Not selected tab|[[1.3.1_Avrundning och värdesiffror|Avrundning & värdesiffror]]}}
 
{{Not selected tab|[[1.3.1_Avrundning och värdesiffror|Avrundning & värdesiffror]]}}
−
{{Not selected tab|[[1.3 Quiz till Decimaltal|Quiz]]}}
 
−
{{Not selected tab|[[1.3 Övningar till Decimaltal|Övningar]]}}
 
−
{{Selected tab|[[1.3 Lathund till Decimaltal|Lathund]]}}
 
−
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
−
|}
 
−
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
−
| style="border-bottom:1px solid #797979" width="5px" | &nbsp;
 
−
{{Not selected tab|[[1.2 Räkneordning| <<&nbsp;&nbsp;Förra avsnitt]]}}
 
−
{{Not selected tab|    }}
 
−
{{Not selected tab|    }}
 
−
{{Not selected tab|    }}
 
 
{{Not selected tab|[[1.4 Negativa tal|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 
{{Not selected tab|[[1.4 Negativa tal|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
 +
:::[[1.2 Räkneordning|<b> <<&nbsp;&nbsp;Förra avsnitt</b>]]
  
−
== <b><span style="color:#931136">Decimaltal</span></b> ==
+
= <b><span style="color:#931136">Tal i decimalform = Tal mellan två [[1.1_Om_tal#Olika_typer_av_tal|<span style="color:blue">heltal</span>]] </span></b> =
−
<br>
+
 
<div class="border-divblue">
 
<div class="border-divblue">
 +
 +
Fortsättning på det [[1.1_Om_tal#Exempel_1|<b><span style="color:blue">decimala positionssystemet</span></b>]]:
 +
 
<big>
 
<big>
 
[[Image: Decimaltal_60a.jpg]]
 
[[Image: Decimaltal_60a.jpg]]
−
 
  
  
Rad 39: Rad 33:
  
  
−
== <b><span style="color:#931136">Exempel på viktiga decimaltal</span></b> ==
+
= <b><span style="color:#931136">Heltal i decimalform</span></b> =
−
<br>
+
Ex
 
<div class="ovnE">
 
<div class="ovnE">
 +
<big><math> 7\,142 \; = \; 7\,142 \, {\bf{\color{Red},}} \, {\color{LimeGreen} {000\, \ldots}} </math></big>
 +
</div>
 +
 +
 
<big>
 
<big>
 +
Generellt
 +
<div class="border-divblue">
 +
Alla heltal kan skrivas i decimalform med <b><span style="color:red">deci-</span></b>
 +
 +
<b><span style="color:red">maltecknet</span></b> och <b><span style="color:green">nollor</span></b> som decimaler. Slut-
 +
 +
sats: Alla heltal är decimaltal, men inte tvärtom.
 +
</div>
 +
</big>
 +
 +
 +
= <b><span style="color:#931136">Exempel på viktiga decimaltal</span></b> =
 +
<br>
 +
<div class="ovnE">
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 52: Rad 64:
 
<math> \displaystyle{ 0,75 \, = \, {3 \over 4} } </math>
 
<math> \displaystyle{ 0,75 \, = \, {3 \over 4} } </math>
 
</td>
 
</td>
−
<td> <math> \qquad\quad </math> </td>
+
<td> <math> \qquad\qquad </math> </td>
 
<td>
 
<td>
 
<math> \displaystyle{ 0,1 \, = \, {1 \over 10} } </math>
 
<math> \displaystyle{ 0,1 \, = \, {1 \over 10} } </math>
Rad 65: Rad 77:
  
 
<math> \qquad\quad \displaystyle{ 0,666\,666\,\ldots \, = \, {2 \over 3} } </math>
 
<math> \qquad\quad \displaystyle{ 0,666\,666\,\ldots \, = \, {2 \over 3} } </math>
−
</big></div>
+
</div>
 +
 
 +
 
 +
= <b><span style="color:#931136">Placering av decimaltal på tallinjen</span></b> =
 +
<div class="ovnC">
 +
<big>
 +
<b><span style="color:#931136">Ex.:</span></b> &nbsp; Vilket decimaltal pekar pilen på?
 +
 
 +
::[[Image: Decimaltallinje_60.jpg]]
 +
 
 +
<b><span style="color:#931136">Lösning:</span></b>
 +
 
 +
Vi befinner oss på den negativa delen av tallinjen.
 +
 
 +
Det sökta decimaltalet ligger mellan heltalen <math> \, -4 \, </math> och <math> \, -5 </math>.
 +
 
 +
[[Image: Decimaltallinje_Svar_60b.jpg]]
 +
 
 +
Ett streck på tallinjen<span>:</span> <math> 1/4 = {1 \over 4} = {1 \cdot {\color{Red} {25}} \over 4 \cdot {\color{Red} {25}}} = {25 \over 100} \, = \, 0,25 </math>
 +
 
 +
Starta vid <math> \, -4 \, </math> och gå tre steg till vänster <span>:</span>
 +
 
 +
<math> \, -4 \,-\, 0,25 \,-\, 0,25 \,-\, 0,25 \, = \, {\color{Red} {-4,75}}</math>.
 +
</big></div>
 +
 
 +
 
 +
= <b><span style="color:#931136">Avrundningsregeln</span></b> =
 +
<br>
 +
<div class="border-divblue">
 +
<big>
 +
Om siffran <u>efter</u> avrundningssiffran är:
 +
</big>
 +
 
 +
<math> \quad\; 0, \, 1, \, 2, \, 3 \; {\rm eller} \; 4 , \quad </math> avrunda <b><span style="color:red">nedåt</span></b>.
 +
 
 +
<math> \quad\; 5, \, 6, \, 7, \, 8 \; {\rm eller} \; 9 , \quad </math> avrunda <b><span style="color:red">uppåt</span></b>.
 +
 
 +
Avrundningssiffran är den siffra efter vilken
 +
 
 +
alla decimaler ska kapas av.
 +
</div>
 +
 
 +
 
 +
== <b><span style="color:#931136">Värdesiffror</span></b> ==
 +
<br>
 +
<div class="border-divblue">
 +
 
 +
{|class="wikitable"
 +
!&nbsp;&nbsp;&nbsp;Tal&nbsp;&nbsp;&nbsp;!!&nbsp;&nbsp;&nbsp;Antal <b><span style="color:red">värdesiffror</span></b>&nbsp;&nbsp;&nbsp;
 +
|-
 +
|align="left"|<math> \qquad 3,14 \quad </math> || align="center"|<b>Tre</b>
 +
|-
 +
|align="left"|<math> \qquad 0,05 \quad </math> || align="center"|<b>En</b>
 +
|-
 +
|align="left"|<math> \qquad 0,072 \quad </math> || align="center"|<b>Två</b>
 +
|-
 +
|align="left"|<math> \qquad 0,40300 \quad </math> || align="center"|<b>Fem</b>
 +
|-
 +
|align="left"|<math> \qquad 1,006 \, </math> || align="center"|<b>Fyra</b>
 +
|}
 +
</div>
  
  
Rad 71: Rad 143:
 
<br>
 
<br>
 
<div class="ovnC">
 
<div class="ovnC">
−
<big>Skriv <math> \; 0,75 \; </math> i bråkform.
+
<big>Skriv <math> \; 0,75 \; </math> i bråkform.</big>
  
−
<math> 0,75 \, = \, \displaystyle {75 \over 100} \, = \, {15 \cdot \cancel{\color{Red} 5} \over 20 \cdot \cancel{\color{Red} 5}} \, = \, {15  \over 20} \, = \, </math>
+
<b>Lösning:</b>
  
−
<math> \qquad\; = \, \displaystyle {3 \cdot \cancel{\color{Red} 5} \over 4 \cdot \cancel{\color{Red} 5}} \, = \, = \, {3 \over 4} </math>  
+
<math> 0,75 \, = \, \displaystyle {75 \over 100} \, = \, {15 \cdot \cancel{\color{Red} 5} \over 20 \cdot \cancel{\color{Red} 5}} \, = \, {15  \over 20} \, = </math>
  
−
Metoden:
+
<math> \qquad\; = \; \displaystyle {3 \cdot \cancel{\color{Red} 5} \over 4 \cdot \cancel{\color{Red} 5}}  \; = \; {3 \over 4} </math>
  
−
<small>
+
<b>Metoden:
−
<b>1.</b> &nbsp; Skriv som bråk med <math> 10</math>-potens i nämnaren.
+
 
 +
1.</b> &nbsp; Skriv som bråk med <math> 10</math>-potens i nämnaren.
  
 
<b>2. &nbsp; <span style="color:red">Förkorta</span></b> bråket så långt som möjligt.
 
<b>2. &nbsp; <span style="color:red">Förkorta</span></b> bråket så långt som möjligt.
−
</small>
+
</div>
−
</big></div>
+
  
  
Rad 90: Rad 162:
 
<br>
 
<br>
 
<div class="ovnC">
 
<div class="ovnC">
−
<big>Skriv <math> \; \displaystyle{3 \over 4} \; </math> som decimaltal.
+
<big>Skriv <math> \; \displaystyle{3 \over 4} \; </math> som decimaltal.</big>
  
−
<math> \displaystyle {3 \over 4} \, = \, {3 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \, = \, {15 \over 20} \, = \, {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \, = \, </math>
+
<b>Lösning:</b>
  
−
<math> \quad\; = \, \displaystyle {75 \over 100} \, = \, 0,75 </math>
+
<math> \displaystyle {3 \over 4} \; = \; {3 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \; = \; {15 \over 20} \; = \; {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \; = \displaystyle {75 \over 100} \; = </math>
  
−
Metoden:
+
<math> \quad\; = \; 0,75 </math>
  
−
<small>
+
<b>Metoden:
−
<b>1. &nbsp; <span style="color:red">Förläng</span></b> bråket tills nämnaren blir en <math> 10</math>-potens.
+
 
 +
1. &nbsp; <span style="color:red">Förläng</span></b> bråket tills nämnaren blir en <math> 10</math>-
 +
 
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; potens.
  
 
<b>2.</b> &nbsp; Skriv resultatet från <b>1</b> till decimaltal.
 
<b>2.</b> &nbsp; Skriv resultatet från <b>1</b> till decimaltal.
−
</small>
+
</div>
−
</big></div>
+
  
  
−
== <b><span style="color:#931136">Periodisk decimalutveckling</span></b> ==
+
= <b><span style="color:#931136">Periodisk decimalutveckling</span></b> =
 
<br>
 
<br>
−
<div class="ovnA">
+
<div class="ovnE">
−
<b><span style="color:#931136">a)</span></b>&nbsp;&nbsp;&nbsp;Skriv <math> \; 0,333\,333\,\ldots \; </math> i bråkform.
+
<big>Skriv <math> \; 0,333\,333\,\ldots \; </math> i bråkform.</big>
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<b><span style="color:#931136">Lösning:</span></b> <math> \quad \quad\; 10 \; \cdot \; 0,333\,333\,\ldots \; = \; 3,333\,333\,\ldots \qquad\qquad {\rm (I)} </math>
+
<b>Lösning:</b>
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<span style="color:#F2F2F2">Lösning:</span> <math> \quad\;\;\, \underline{\quad\; 1 \;\, \cdot \; 0,333\,333\,\ldots \; = \; 0,333\,333\,\ldots} \qquad\qquad {\rm (II)} </math>
+
<math> 10 \; \cdot \; 0,333\,333\,\ldots \; = \; 3,333\,333\,\ldots \quad {\rm (I)} </math>
  
−
::<math>\;\;{\rm (I)-(II)} \quad\quad\! 9 \;\; \cdot \; 0,333\,333\,\ldots \; = \; 3 </math>
+
<math> \underline{\;1 \;\, \cdot \; 0,333\,333\,\ldots \; = \; 0,333\,333\,\ldots} \quad {\rm (II)} </math>
  
−
:::::::<math> \quad\;\;\, 0,333\,333\,\ldots \: = \: \displaystyle{3 \over 9} \; = \; {1 \cdot \cancel{\color{Red} 3} \over 3 \cdot \cancel{\color{Red} 3}} </math>
+
Vi bildar <math> \; {\rm (I)-(II)} </math><span style="color:black">:</span>
  
−
:::::::<math> \quad\;\;\, 0,333\,333\,\ldots \: = \: \displaystyle{1 \over 3} </math>
+
<math> (10-1) \cdot 0,333\,\ldots = \; 3 </math>
 +
 
 +
<math> \quad\;\;\; 9 \quad\, \cdot \, 0,333\ldots = \; 3 </math>
 +
 
 +
<math> \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{3 \over 9} \; = \; {1 \cdot \cancel{\color{Red} 3} \over 3 \cdot \cancel{\color{Red} 3}} </math>
 +
 
 +
<math> \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{1 \over 3} </math>
 
</div>
 
</div>
 +
 +
 +
<div class="border-divblue">
 +
 +
{|class="wikitable"
 +
!&nbsp;&nbsp;&nbsp;Tal&nbsp;&nbsp;&nbsp;!!&nbsp;&nbsp;&nbsp;<b><span style="color:red">Perioden</span></b>&nbsp;&nbsp;&nbsp;!!&nbsp;Skrivsätt&nbsp;
 +
|-
 +
|align="left"|<math> \;\; 0,333\,333\,\ldots </math> || align="center"|<b>3</b> || align="center"|<math> 0,\bar{3} </math>
 +
|-
 +
|align="left"|<math> \;\; 0,666\,666\,\ldots </math> || align="center"|<b>6</b> || align="center"|<math> 0,\bar{6} </math>
 +
|-
 +
|align="left"|<math> \;\; 0,18181818\,\ldots </math> || align="center"|<b>18</b> || align="center"|<math> 0,\overline{18} </math>
 +
|-
 +
|align="left"|<math> \;\; 1,16666666\,\ldots </math> || align="center"|<b>6</b> || align="center"|<math> 1,1\bar{6} </math>
 +
|-
 +
|align="left"|<math> \;\; 0,09090909\,\ldots </math> || align="center"|<b>09</b> || align="center"|<math> 0,\overline{09} </math>
 +
|-
 +
|align="left"|<math> \;\; 0,045454545\,\ldots </math> || align="center"|<b>45</b> || align="center"|<math> 0,0\overline{45} </math>
 +
|}
 +
</div>
 +
 +
 +
= <b><span style="color:#931136">Icke-periodisk decimalutveckling</span></b> =
 +
<div class="ovnA">
 +
<big>
 +
Så kallas tal som har oändligt många decimaler utan
 +
 +
något upprepande mönster (utan period), t.ex.: 
 +
 +
::<math>\sqrt{2} \; = \; 1,4142135623730950488016887\ldots \, </math>
 +
 +
Detta decimaltal är en icke-periodisk decimalutveckling,
 +
 +
för det har oändligt många decimaler utan period, dvs
 +
 +
utan grupper av siffror som upprepas. Man kallar dem
 +
 +
för irrationella. <math> \sqrt{2} \, </math> är ett exempel på ett irrationellt tal.
 +
 +
Ändå är <math> \sqrt{2} \cdot \sqrt{2} = 2 \, </math> ett heltal, se [[1.1_Om_tal#Olika_typer_av_tal|<b><span style="color:blue">Olika typer av tal</span></b>]].
 +
 +
Ett annat exempel är talet [[1.3 Decimaltal#Viktiga_decimaltal|<b><span style="color:blue"><big><math> \, \pi </math></big></span></b>]]. Det finns oändligt
 +
 +
många irrationella tal. De kan inte skrivas i bråkform.
 +
 +
Det enda sättet att hantera dem är att avrunda dem.
 +
 +
Hur man gör det visas i [[1.3.1_Avrundning_och_värdesiffror|<b><span style="color:blue">Avrundning och värdesiffror</span></b>]].
 +
</big></div>
 +
  
  
Rad 128: Rad 258:
  
  
−
[[Matte:Copyrights|Copyright]] © 2010-2017 Math Online Sweden AB. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2023 <b><span style="color:blue">TechPages AB</span></b>. All Rights Reserved.

Nuvarande version från 15 januari 2023 kl. 19.11

       Genomgång          Quiz          Övningar          Avrundning & värdesiffror          Nästa avsnitt  >>      
<<  Förra avsnitt

Tal i decimalform = Tal mellan två heltal

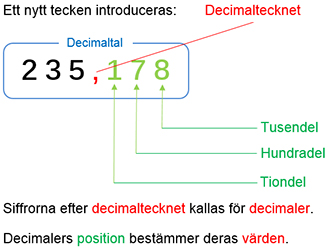
Fortsättning på det decimala positionssystemet:

Decimaltal 60a.jpg


Tiondelssiffran \( \quad\, {\color{LimeGreen} 1} \, \) har värdet \( \, {\color{Red}{0,1}} \, \).

Hundradelssiffran \( {\color{LimeGreen} 7} \, \) har värdet \( \, {\color{Red}{0,07}} \, \).

Tusendelssiffran \( \;\, {\color{LimeGreen} 8} \, \) har värdet \( \, {\color{Red}{0,008}} \, \).

\( 235 \, + \, {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} = \boxed{235\,{\bf{\color{Red},}}\,{\color{LimeGreen} {178}}} \)


Heltal i decimalform

Ex

\( 7\,142 \; = \; 7\,142 \, {\bf{\color{Red},}} \, {\color{LimeGreen} {000\, \ldots}} \)


Generellt

Alla heltal kan skrivas i decimalform med deci-

maltecknet och nollor som decimaler. Slut-

sats: Alla heltal är decimaltal, men inte tvärtom.


Exempel på viktiga decimaltal


\( \displaystyle{ 0,5 \, = \, {1 \over 2} } \)

\( \displaystyle{ 0,25 \, = \, {1 \over 4} } \)

\( \displaystyle{ 0,75 \, = \, {3 \over 4} } \)

\( \qquad\qquad \)

\( \displaystyle{ 0,1 \, = \, {1 \over 10} } \)

\( \displaystyle{ 0,01 \, = \, {1 \over 100} } \)

\( \displaystyle{ 0,001 \, = \, {1 \over 1000} } \)

\( \qquad\quad \displaystyle{ 0,333\,333\,\ldots \, = \, {1 \over 3} } \)

\( \qquad\quad \displaystyle{ 0,666\,666\,\ldots \, = \, {2 \over 3} } \)


Placering av decimaltal på tallinjen

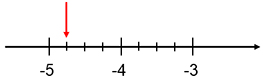
Ex.:   Vilket decimaltal pekar pilen på?

Decimaltallinje 60.jpg

Lösning:

Vi befinner oss på den negativa delen av tallinjen.

Det sökta decimaltalet ligger mellan heltalen \( \, -4 \, \) och \( \, -5 \).

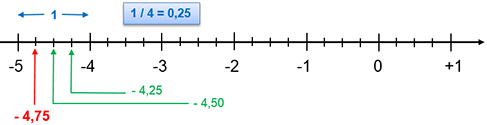
Decimaltallinje Svar 60b.jpg

Ett streck på tallinjen: \( 1/4 = {1 \over 4} = {1 \cdot {\color{Red} {25}} \over 4 \cdot {\color{Red} {25}}} = {25 \over 100} \, = \, 0,25 \)

Starta vid \( \, -4 \, \) och gå tre steg till vänster :

\( \, -4 \,-\, 0,25 \,-\, 0,25 \,-\, 0,25 \, = \, {\color{Red} {-4,75}}\).


Avrundningsregeln


Om siffran efter avrundningssiffran är:

\( \quad\; 0, \, 1, \, 2, \, 3 \; {\rm eller} \; 4 , \quad \) avrunda nedåt.

\( \quad\; 5, \, 6, \, 7, \, 8 \; {\rm eller} \; 9 , \quad \) avrunda uppåt.

Avrundningssiffran är den siffra efter vilken

alla decimaler ska kapas av.


Värdesiffror


   Tal       Antal värdesiffror   
\( \qquad 3,14 \quad \) Tre
\( \qquad 0,05 \quad \) En
\( \qquad 0,072 \quad \) Två
\( \qquad 0,40300 \quad \) Fem
\( \qquad 1,006 \, \) Fyra


Från decimaltal till bråk


Skriv \( \; 0,75 \; \) i bråkform.

Lösning:

\( 0,75 \, = \, \displaystyle {75 \over 100} \, = \, {15 \cdot \cancel{\color{Red} 5} \over 20 \cdot \cancel{\color{Red} 5}} \, = \, {15 \over 20} \, = \)

\( \qquad\; = \; \displaystyle {3 \cdot \cancel{\color{Red} 5} \over 4 \cdot \cancel{\color{Red} 5}} \; = \; {3 \over 4} \)

Metoden:

1.   Skriv som bråk med \( 10\)-potens i nämnaren.

2.   Förkorta bråket så långt som möjligt.


Från bråk till decimaltal


Skriv \( \; \displaystyle{3 \over 4} \; \) som decimaltal.

Lösning:

\( \displaystyle {3 \over 4} \; = \; {3 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \; = \; {15 \over 20} \; = \; {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \; = \displaystyle {75 \over 100} \; = \)

\( \quad\; = \; 0,75 \)

Metoden:

1.   Förläng bråket tills nämnaren blir en \( 10\)-

      potens.

2.   Skriv resultatet från 1 till decimaltal.


Periodisk decimalutveckling


Skriv \( \; 0,333\,333\,\ldots \; \) i bråkform.

Lösning:

\( 10 \; \cdot \; 0,333\,333\,\ldots \; = \; 3,333\,333\,\ldots \quad {\rm (I)} \)

\( \underline{\;1 \;\, \cdot \; 0,333\,333\,\ldots \; = \; 0,333\,333\,\ldots} \quad {\rm (II)} \)

Vi bildar \( \; {\rm (I)-(II)} \):

\( (10-1) \cdot 0,333\,\ldots = \; 3 \)

\( \quad\;\;\; 9 \quad\, \cdot \, 0,333\ldots = \; 3 \)

\( \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{3 \over 9} \; = \; {1 \cdot \cancel{\color{Red} 3} \over 3 \cdot \cancel{\color{Red} 3}} \)

\( \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{1 \over 3} \)


   Tal       Perioden     Skrivsätt 
\( \;\; 0,333\,333\,\ldots \) 3 \( 0,\bar{3} \)
\( \;\; 0,666\,666\,\ldots \) 6 \( 0,\bar{6} \)
\( \;\; 0,18181818\,\ldots \) 18 \( 0,\overline{18} \)
\( \;\; 1,16666666\,\ldots \) 6 \( 1,1\bar{6} \)
\( \;\; 0,09090909\,\ldots \) 09 \( 0,\overline{09} \)
\( \;\; 0,045454545\,\ldots \) 45 \( 0,0\overline{45} \)


Icke-periodisk decimalutveckling

Så kallas tal som har oändligt många decimaler utan

något upprepande mönster (utan period), t.ex.:

\[\sqrt{2} \; = \; 1,4142135623730950488016887\ldots \, \]

Detta decimaltal är en icke-periodisk decimalutveckling,

för det har oändligt många decimaler utan period, dvs

utan grupper av siffror som upprepas. Man kallar dem

för irrationella. \( \sqrt{2} \, \) är ett exempel på ett irrationellt tal.

Ändå är \( \sqrt{2} \cdot \sqrt{2} = 2 \, \) ett heltal, se Olika typer av tal.

Ett annat exempel är talet \( \, \pi \). Det finns oändligt

många irrationella tal. De kan inte skrivas i bråkform.

Det enda sättet att hantera dem är att avrunda dem.

Hur man gör det visas i Avrundning och värdesiffror.





Copyright © 2023 TechPages AB. All Rights Reserved.

Hämtad från "https://matte1b.mathonline.se/index.php?title=1.3_Tal_i_decimalform&oldid=38480"