Skillnad mellan versioner av "3.3 Ekvationer 2 kolumner"

Från Mathonline
Hoppa till: navigering, sök
m
m (Taifun flyttade sidan 3.3 Ekvationer till 3.3 Ekvationer 2 kolumner utan att lämna en omdirigering)
 
(431 mellanliggande versioner av samma användare visas inte)
Rad 2: Rad 2:
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
 +
{{Not selected tab|[[3.2 Förenkling av uttryck| <<&nbsp;&nbsp;Förra avsnitt]]}}
 
{{Selected tab|[[3.3 Ekvationer|Genomgång]]}}
 
{{Selected tab|[[3.3 Ekvationer|Genomgång]]}}
 
{{Not selected tab|[[3.3 Quiz till Ekvationer|Quiz]]}}
 
{{Not selected tab|[[3.3 Quiz till Ekvationer|Quiz]]}}
 
{{Not selected tab|[[3.3 Övningar till Ekvationer|Övningar]]}}
 
{{Not selected tab|[[3.3 Övningar till Ekvationer|Övningar]]}}
−
{{Not selected tab|[[3.3 Lathund till Ekvationer|Lathund]]}}
+
<!-- {{Not selected tab|[[3.3 Ekvationer+|Genomgång+]]}} -->
 +
{{Not selected tab|[[3.4 Ekvationer med x på båda sidor|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
−
== <b><span style="color:#931136">Varför ekvationer?</span></b> ==
+
<table>
−
 
+
<tr>
 +
  <td><div class="border-divblue"><big><big><b><span style="color:#931136">Varför ekvationer?</span></b></big></big></div>
 +
<br>
 
<div class="ovnE">
 
<div class="ovnE">
−
 
+
<b>Exempel på en textuppgift:</b>
−
<b>Ex.:</b>
+
<br>
 
<div class="exempel">
 
<div class="exempel">
−
:Kalle köper en flaska dryck som kostar <math> \, 18 \, </math> kr <u>med</u> pant.
+
:Kalle köper en flaska dryck som kostar <math> \, 18 \, </math> kr <i>med</i> pant.
  
 
:Drycken (innehållet) kostar <math> \, 14 \, </math> kr mer än panten (flaskan).
 
:Drycken (innehållet) kostar <math> \, 14 \, </math> kr mer än panten (flaskan).
  
−
:Hur mycket kommer Kalle att få för panten när han lämnar tillbaka flaskan?
+
:Hur mycket kostar flaskan?
−
 
+
−
:Försök att lösa uppgiften utan ekvation. Lös sedan med ekvation.
+
 
</div>
 
</div>
  
−
[[Användning_av_ekvationer|<b><span style="color:blue">Att ställa upp en ekvation</span></b>]].
+
<b>Utan ekvation</b> svarar de flesta 4 kr, vilket är fel.
  
−
Lösning med ekvation<span style="color:black">:</span> <math> \quad\;\; x \; = \; {\rm flaskans\;pris} </math>
+
<b>Lösning med ekvation:</b> <math> \quad\;\;\; x \; = \; {\rm flaskans\;pris} </math>
−
 
+
−
::::::<math> \;\; x \, + \, 14 \; = \; {\rm dryckens\;pris} </math>
+
  
 +
::::<math> \qquad\qquad\;\; x \, + \, 14 \; = \; {\rm dryckens\;pris} </math>
 
<div class="exempel">
 
<div class="exempel">
−
::<math>\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18                                       &          &                        \\
+
::::::<math>\begin{array}{rcl} x \, + \, (x \, + \, 14) & = & 18           \\
−
                              x \, + \, x \, + \, 14 & = & 18                                       &          &                        \\
+
                                x \, + \, x \, + \, 14 & = & 18           \\
−
                                      2\,x \, + \, 14 & = & 18                                       & \qquad | & {\color{Red} {- \, 14}} \\
+
                                        2\,x \, + \, 14 & = & 18           \\
−
          2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}}             &          &                        \\
+
                                        2\,x \,       & = & 4             \\
−
                                      2\,x \,       & = & 4                                        & \qquad | & {\color{Red} {/ \; 2}}  \\
+
                                          x \,         & = & {\color{Red} 2}   
−
        \displaystyle \frac{2\,x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} &          &                        \\
+
−
                                        x \,        & = & 2                                        &          &
+
 
           \end{array}</math>
 
           \end{array}</math>
 
</div>
 
</div>
  
−
Skrivsättet <math> \quad | \quad {\color{Red} {- \, 14}} \quad\!</math> betyder att <math> \, 14 \, </math> ska subtraheras från ekvationens båda led.
 
  
−
Skrivsättet <math> \quad | \quad {\color{Red} {/ \; 2}} \quad\;\; </math> betyder att ekvationens båda led ska divideras med <math> \, 2 \, </math>.
+
<b>Svar:</b> &nbsp;&nbsp;&nbsp; Flaskan kostar <math> \, {\color{Red} {2 \; {\rm kr\,}}}</math>.
  
  
−
<b>Svar:</b> &nbsp;&nbsp;&nbsp; Kalle kommer att få <math> \, 2 \; {\rm kr} \, </math> för panten när han lämnar tillbaka flaskan.
+
För mer info om hur man ställer upp en ekvation och om lösningsmetoder se:
  
  
 +
[[3.6_Användning_av_ekvationer#Metoden_att_st.C3.A4lla_upp_en_ekvation_utifr.C3.A5n_en_textuppgift|<b><span style="color:blue">Metoden att ställa upp en ekvation utifrån en textuppgift</span></b>]],
 +
 +
[[3.3_Ekvationer#1._.C2.A0_.C3.96vert.C3.A4ckningsmetoden|<b><span style="color:blue">Övertäckningsmetoden</span></b>]] <math> \quad </math> och <math> \quad </math> [[3.3_Ekvationer#2._.C2.A0_Allm.C3.A4n_metod|<b><span style="color:blue">Allmän metod</span></b>]].
 
</div>
 
</div>
 +
</td>
 +
  <td><math> \;\; </math></td>
 +
  <td> <div class="border-divblue"><big><big><b><span style="color:#931136">Vad är en ekvation?</span></b></big></big></div>
 +
<br>
 +
<math> \qquad\quad </math>[[Image: Ekvation Obekant VL HL_350.jpg]]
 +
<br>
 +
<div class="border-divblue">
 +
<big>
 +
En <b><span style="color:#931136">ekvation</span></b> är en likhet mellan två uttryck,
  
 +
har alltid formen VL = HL och innehåller
  
−
<div class="tolv"> <!-- tolv1 -->
+
minst en variabel, kallad <b>obekant</b>.
−
Felet beror på att man blandar ihop två olika räkneoperationer: multiplikationen med <strong><span style="color:red">upphöjt till</span></strong>.
+
  
−
Hjärnan associerar <math> \, 2 \, </math> och <math> \, 3 \, </math> blind till multiplikationstabellen och ger <math> \, 6 </math> vilket är fel.
+
Ex.<span style="color:black">:</span> <math> \qquad\quad 2\,x \; + \; 14 \; = \; 18 </math>
  
−
I själva verket betyder <math> \, 2\,^{\color{Red} 3} \, </math> inte <math> \, 2 \cdot 3 \, </math> utan <math> \, \underbrace{2 \cdot 2 \cdot 2}_{{\color{Red} 3}\;\times} \, </math> som sedan förkortas till <math> \, 2\,^{\color{Red} 3} </math>.
+
Ekvationens <b><span style="color:red">lösning:</span></b> <math> \quad\; </math> <div class="smallBoxVariantt"> <math> x \; = \; {\color{Red} 2} </math></div>
−
</div> <!-- tolv1 -->
+
−
 
+
−
<table>
+
−
<tr>
+
−
  <td><div class="border-divblue">
+
−
<big>Exempel på potens:
+
−
 
+
−
::<math> 2\,^{\color{Red} 3} \; = \;\; \underbrace{2 \, \cdot \, 2 \, \cdot \, 2}_{{\color{Red} 3}\;\times} </math>  
+
−
 
+
−
<span style="color:#931136">Potens</span> = upprepad multiplikation
+
−
 
+
−
av <math> \, 2 \, </math> med sig själv, <math> \, {\color{Red} 3} \, </math> gånger.
+
 
</big></div>
 
</big></div>
−
</td>
 
−
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Potens Bas Exponent_80.jpg]]</td>
 
−
</tr>
 
−
</table>
 
  
  
−
<div class="tolv"> <!-- tolv2 -->
+
:<big><big><big><b><span style="color:#931136">Varför lösning?</span></b></big></big></big>
−
<math> \, 2\,^3 \, </math> läses <math> \, {\color{Red} 2} </math> <strong><span style="color:red">upphöjt till</span></strong><math> \, {\color{Red} 3} \, </math> och kallas för &nbsp;<strong><span style="color:red">potens</span></strong>. <math> \, 2\, </math> heter <strong><span style="color:red">basen</span></strong> och <math> \, 3 \, </math> <strong><span style="color:red">exponenten</span></strong>.
+
  
−
Exponenten <math> \, {\color{Red} 3} \, </math> är inget tal i vanlig bemärkelse utan endast en information om att <math> \, 2 \, </math> ska multipliceras <math> \, {\color{Red} 3} \, </math> gånger med sig själv  (jfr. [[1.2_Räkneordning#Varf.C3.B6r_g.C3.A5r_multiplikation_f.C3.B6re_addition.3F|<strong><span style="color:blue">upprepad addition</span></strong>]]).
+
<div class="border-divblue">
−
</div> <!-- tolv2 -->
+
−
 
+
−
 
+
−
<div class="exempel"> <!-- exempel1 -->
+
−
== <b><span style="color:#931136">Exempel 1</span></b> ==
+
 
<big>
 
<big>
−
Förenkla<span style="color:black">:</span> <math> \qquad \displaystyle{2\,^3 \cdot \; 2\,^5 \over 2\,^4} </math>
+
<b><span style="color:#931136">Kontroll:</span></b> Sätt in lösningen i ekvationen.
  
 +
VL <math> \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 </math>
  
−
<strong><span style="color:#931136">Lösning:</span></strong> <math> \qquad \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \over 2 \cdot 2 \cdot 2 \cdot 2} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot \cancel{2 \cdot 2 \cdot 2 \cdot 2} \over \cancel{2 \cdot 2 \cdot 2 \cdot 2}} \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} </math>
+
HL <math> \, = \, 18 </math>
  
−
:::::::::::::::::OBS! &nbsp; Förenkla alltid först, räkna sedan!
+
<b>VL <math> = </math> HL</b> <math> \, \implies \, x = {\color{Red} 2} </math> är en <b><span style="color:red">lösning</span></b>.
  
−
Snabbare<span style="color:black">:</span> <math> \qquad\!\! \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, 2\,^{3\,+\,5\,-\,4} \, = \, 2\,^4 \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} </math>
+
<b><span style="color:#931136">Kontroll</span></b> kallas ibland även för <b><span style="color:#931136">prövning.</span></b>
 
</big>
 
</big>
−
</div> <!-- exempel1 -->
+
</div>
 +
</td>
 +
</tr>
 +
</table>
  
  
−
<div class="tolv"> <!-- tolv2 -->
+
<big><big>Om kontrollen ovan säger man: Lösningen <b><span style="color:red">satisfierar</span></b> (uppfyller) ekvationen.</big></big>
−
För att förstå den snabbare lösningen se [[1.7_Potenser#Potenslagarna|<strong><span style="color:blue">potenslagarna</span></strong>]].
+
−
</div> <!-- tolv2 -->
+
  
  
−
== <b><span style="color:#931136">Potens med positiva heltalsexponenter</span></b> ==
+
<big><big>Men hur <b><span style="color:red">får</span></b> man lösningen? Det finns två lösningsmetoder:</big></big>
−
<div class="tolv"> <!-- tolv1 -->
+
  
−
Potensen <big><math> \, a\,^{\color{Red} x} \, </math></big> kan, om exponenten <math> \, {\color{Red} x} \, </math> är ett positivt heltal och basen <big><math> \, a \, </math></big> ett tal <math> \neq 0 </math>, definieras som
 
  
−
::::::<b>Upprepad multiplikation av <big><math> \, a \, </math></big> med sig själv, <math> \, {\color{Red} x} \, </math> gånger:</b>
+
= <b><span style="color:#931136">1. &nbsp; Övertäckningsmetoden</span></b> =
  
−
::::::::<big><math> a\,^{\color{Red} x} = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{{\color{Red} x}\;{\rm gånger}} </math></big>
+
<div class="ovnC">
−
</div> <!-- tolv1 -->
+
<big><b><span style="color:#931136">Exemplet ovan:</span></b>
  
−
<div class="exempel"> <!-- exempel2 -->
+
&nbsp; <math> 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x </math>
−
== <b><span style="color:#931136">Exempel 2</span></b> ==
+
−
<big>
+
−
Förenkla<span style="color:black">:</span> <big><math> \quad\;\; a\,^2 \, \cdot \, a\,^3 </math></big>
+
  
 +
<div class="RedBox2x"><math>\quad</math></div> <math> \, + \;\, 14 \; = \; 18 </math>
  
−
<strong><span style="color:#931136">Lösning:</span></strong>  
+
&nbsp; <math> \;\, {\color{Red} ?} \;\;\; + \; 14 \; = \; 18 </math>
  
−
::::<big><math> a\,^2 \cdot a\,^3 \; = \; \underbrace{a \cdot a}_{2\;\times} \; \cdot \; \underbrace{a \cdot a \cdot a}_{3\;\times} \; = \; \underbrace{a \cdot a \cdot a \cdot a \cdot a}_{{\color{Red} 5}\;\times} \; = \; a\,^{\color{Red} 5}</math></big>
+
&nbsp; <math> \;\, {\color{Red} 4} \;\;\; + \; 14 \; = \; 18 </math>
  
−
Snabbare:
+
&nbsp; <math> \;\, \Downarrow </math>
  
−
::::<big><math> a\,^2 \cdot a\,^3 \; = \; a\,^{2\,+\,3} = \; a\,^{\color{Red} 5} </math></big>
+
&nbsp; <math> \, 2 \, \cdot \; x \;\; = \;\, {\color{Red} 4} \qquad\quad {\color{Red} {\rm Täck\;över\;}} x </math>
−
</big>
+
−
</div> <!-- exempel2 -->
+
  
 +
&nbsp; <math> \, 2 \, \cdot \; </math><div class="RedBoxx"><math> \quad </math></div> <math> \; = \;\, 4 </math>
  
−
<div class="tolv"> <!-- tolv2 -->
+
&nbsp; <math> \, 2 \, \cdot \; {\color{Red} ?} \;\; = \;\; 4 </math>
−
Den snabbare lösningen är ett exempel på den första potenslagen:
+
−
</div> <!-- tolv2 -->
+
  
 +
&nbsp; <math> \, 2 \, \cdot \; {\color{Red} 2} \;\; = \;\; 4 </math>
  
−
== <b><span style="color:#931136">Potenslagarna</span></b> ==
+
&nbsp; <math> \quad\;\;\; \Downarrow </math>
−
<div class="tolv"> <!-- tolv3 -->
+
  
−
Följande lagar gäller för potenser där basen <math> a\, </math> är ett tal <math> \neq 0 </math>, exponenterna <math> \, x \, </math> och <math> \, y \, </math> godtyckliga tal och <math> m,\,n </math> heltal (<math> n\neq 0 </math>):
+
&nbsp; <div class="smallBoxVariantt"> <math> \; x \; = \; {\color{Red} 2} </math></div>
−
</div> <!-- tolv3 -->
+
</big></div>
  
  
−
<div class="border-divblue">
+
= <b><span style="color:#931136">2. &nbsp; Allmän metod</span></b> =
−
<b><span style="color:#931136">Första potenslagen:</span></b> <big><math> \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad </math></big>
+
<div class="ovnE">
−
----
+
<big><b><span style="color:#931136">Exempel:</span></b></big>
−
<b><span style="color:#931136">Andra potenslagen:</span></b> <big><math> \qquad\qquad\qquad\;\;\; \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Tredje potenslagen:</span></b> <big><math> \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Lagen om nollte potens:</span></b> <big><math> \qquad\qquad\quad\;\;\, a\,^0 \; = \; 1 \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Lagen om negativ exponent:</span></b> <big><math> \qquad\quad\;\;\; a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Potens av en produkt:</span></b> <big><math> \qquad\qquad\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Potens av en kvot:</span></b> <big><math> \qquad\qquad\qquad\, \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad </math></big>
+
−
</div> <!-- border-divblue -->
+
  
 +
<div class="exempel">
 +
::<math>\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18                                        &          &                        \\
 +
                              x \, + \, x \, + \, 14 & = & 18                                        &          &                        \\
 +
                                      2\,x \, + \, 14 & = & 18                                        & \qquad | & {\color{Red} {- \, 14}} \\
 +
          2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}}            &          &                        \\
 +
                                2 \cdot x \,        & = & 4                                        & \qquad | & {\color{Red} {/ \; 2}}  \\
 +
    \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & &  \\
 +
                                        x \,        & = & 2                                        &          &
 +
        \end{array}</math>
 +
</div>
  
−
<div class="tolv"> <!-- tolv3a -->
+
Skrivsättet <math> \quad\;\;\, | \quad {\color{Red} {- \, 14}} \quad\;\;\, </math> är en kommentar och betyder<span style="color:black">:</span>
−
För enkelhets skull definierades potensbegreppet inledningsvis endast för positiva heltalsexponenter <math> \, x \, </math> och <math> \, y </math>. Men potenslagarna gäller även för exponenter som är negativa eller bråktal. I formuleringen "negativ exponent" antas <math> \, x > 0 </math>.
+
−
</div> <!-- tolv3a -->
+
  
 +
::Subtrahera <math> \, 14 \, </math> från ekvationens båda led.
  
−
<div class="exempel"> <!-- exempel3 -->
+
Kommentaren <math> \;\; | \quad {\color{Red} {/ \; 2}} \;\; </math> betyder<span style="color:black">:</span>
−
== <b><span style="color:#931136">Exempel 3</span></b> ==
+
−
<big>
+
  
−
::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; {a \cdot a \cdot a \cdot a \cdot a \; \over \; a \cdot a \cdot a} \; = \; {a \cdot a \cdot \cancel{a \cdot a \cdot a} \; \over \; \cancel{a \cdot a \cdot a}} \; = \; a \cdot a \; = \; a\,^2 </math></big>
+
::Dividera ekvationens båda led med <math> \, 2 </math>.
 +
</div>
  
−
Snabbare med andra potenslagen:
 
  
−
::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5\,-\,3}}} \; = \; a\,^2 </math></big>
+
== <b><span style="color:#931136">Den allmänna metoden steg för steg</span></b> ==
−
</big>
+
−
</div> <!-- exempel3 -->
+
  
 +
<div class="ovnE">
 +
<b>Steg 1</b>
 +
<div class="exempel">
  
−
<div class="tolv"> <!-- tolv2 -->
+
&nbsp; Förenkla uttrycken i ekvationens båda led
−
'''Påstående (Lagen om nollte potens)''':
+
  
−
::::<big><math> a^0 \; = \; 1 </math></big>
+
&nbsp; så långt som möjligt. I exemplet ovan<span style="color:black">:</span>
  
−
'''Bevis''':
+
::<math>\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18  &  &  \\
 +
                              x \, + \, x \, + \, 14 & = & 18  &  &  \\
 +
                                      2\,x \, + \, 14 & = & 18  &  & 
 +
        \end{array}</math>
 +
</div>
  
−
Påståendet kan bevisas genom att använda andra potenslagen:
+
<b>Steg 2</b>
 +
<div class="exempel">
  
−
::::<big><math> \displaystyle{a^x \over a^x} \; = \; a^{x-x} \; = \; a^0 </math></big>
+
&nbsp; Utför <b><span style="color:red">samma operation</span></b> på båda leden<span style="color:black">:</span>  
  
−
Å andra sidan vet vi att ett bråk med samma täljare som nämnare har värdet <math> \, 1 </math>:
+
::<math>\begin{array}{rcl}          2\,x \, + \, 14 & = & 18                            \\
 +
        2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} \\
 +
                                            2\,x \, & = & 4
 +
        \end{array}</math>
  
−
::::<big><math> \displaystyle{a^x \over a^x} \; = \; 1 </math></big>
+
<b><span style="color:red">Vilken operation?</span></b>
  
−
Av raderna ovan följer påståendet:
+
<b>Den inversa operation som isolerar <math> x</math>-termen. </b>
  
−
::::<big><math> a^0 \; = \; 1 </math></big>
+
<math> \;\;\; {\color{Red} {- \, 14}} \, </math> är den <b><span style="color:red">inversa operationen</span></b> till <math> \, + \, 14 </math>
−
</div> <!-- tolv4 -->
+
</div>
  
 +
<b>Steg 3</b>
 +
<div class="exempel">
  
−
<div class="exempel"> <!-- exempel4 -->
+
&nbsp; Utför <b><span style="color:red">samma operation</span></b> på båda leden<span style="color:black">:</span>  
−
== <b><span style="color:#931136">Exempel på potenser med negativa exponenter</span></b> ==
+
−
<big>
+
  
−
::::<math> \displaystyle{10\,^{-1} \, = \, {1 \over 10\,^1} \, = \, {1 \over 10} \, = \, 0,1} </math>
+
::::<math>\begin{array}{rclcl} \quad\;  2 \cdot x \, & = & 4                                        &  & \\
 +
    \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} &  & \\
 +
                                                    x & = & 2                                        &  &
 +
          \end{array}</math>
  
−
::::<math> \displaystyle{10\,^{-2} \, = \, {1 \over 10\,^2} \, = \, {1 \over 10 \cdot 10} \, = \, {1 \over 100} \, = \, 0,01} </math>
+
<b><span style="color:red">Vilken operation?</span></b>
  
−
::::<math> \displaystyle{10\,^{-3} \, = \, {1 \over 10\,^3} \, = \, {1 \over 10 \cdot 10 \cdot 10} \, = \, {1 \over 1000} \, = \, 0,001} </math>
+
<b>Den inversa operation som isolerar <math> \, x \, </math>. </b>
−
</big>
+
−
</div> <!-- exempel4 -->
+
  
 +
<math> \quad\;\; {\color{Red} {/ \; 2}} \, </math> är den <b><span style="color:red">inversa operationen</span></b> till <math> \, \cdot \; 2 </math>
 +
</div>
  
−
<div class="tolv"> <!-- tolv4a -->
 
  
−
'''Påstående (Lagen om negativ exponent, <math> \, x > 0 </math>)''':
+
</div>
  
−
::::<big><math> a^{-x} = \displaystyle{1 \over a^x} </math></big>
 
  
−
'''Bevis''':
+
<div class="border-divblue">
−
 
+
−
Påståendet kan bevisas genom att använda lagen om nollte potensen (baklänges) samt andra potenslagen:
+
−
 
+
−
::::<big><math> \displaystyle{1 \over a^x} \; = \; \displaystyle{a^0 \over a^x} \; = \; a^{0-x} \; = \; a^{-x} </math></big>
+
−
 
+
−
Vi får påståendet, fast baklänges.
+
−
</div> <!-- tolv4a -->
+
−
 
+
−
 
+
−
<div class="tolv"> <!-- tolv5 -->
+
−
Att potenser med negativa exponenter är en naturlig fortsättning på potenser med positiva exponenter med nollte potensen däremellan illustrerar följande exempel:
+
−
</div> <!-- tolv5 -->
+
−
 
+
−
 
+
−
<div class="exempel"> <!-- exempel4 -->
+
−
== <b><span style="color:#931136">Varför är <math> \; 5\,^0 \, = \, 1 \; </math>?</span></b> ==
+
 
<big>
 
<big>
 +
<b><span style="color:#931136">Den allmänna metodens filosofi:</span></b>
  
−
::::<math> \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 </math>
+
Betrakta ekvationen som en <b><span style="color:red">våg i balans</span></b>.
  
−
::::<math> \;\; 5^3 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 </math>
+
HL och VL är vågens skålar. Likhetsteck-
  
−
::::<math> \;\; 5^2 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 </math>
+
net betyder att vågens skålar är i balans.
  
−
::::<math> \;\; 5^1 \; = \; {\color{Red} 1} \cdot 5 </math>
+
Bibehåll balansen genom att utföra<span style="color:black">:</span>
  
−
::::<math> \;\; {\color{Red} {5^0 \; = \; 1}} </math>
+
<math> \;\;\; </math> <b><span style="color:red">Samma operation på båda leden !</span></b>
  
−
::::<math> \;\; 5^{-1} \; = \; \displaystyle{{\color{Red} 1} \over 5} </math>
+
Välj alltid den <b><span style="color:red">inversa</span></b> operationen till den
  
−
::::<math> \;\; 5^{-2} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5} </math>
+
operation som binder <math> \, x \, </math> till dess omgivning.
 +
</big></div>
  
−
::::<math> \;\; 5^{-3} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5} </math>
 
  
−
::::<math> \;\; 5^{-4} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5 \cdot 5 } </math>
+
== <b><span style="color:#931136">När saknar en ekvation lösning?</span></b> ==
  
−
Att <math> \; {\color{Red} 1} </math>-orna följer med hela tiden beror på att multiplikationens ''enhet'' är <math> \, {\color{Red} 1} </math>, dvs <math> \, a \cdot {\color{Red} 1} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 1} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5^0}} \, </math> då alla <math> \, 5</math>-or har försvunnit.
+
<br>
−
</big>
+
−
</div> <!-- exempel4 -->
+
  
 +
<div class="ovnC">
 +
<big><b><span style="color:#931136">Exempel:</span></b></big>
  
−
<div class="tolv"> <!-- tolv5 -->
+
<div class="exempel">
−
Jämför med:
+
<math>\begin{array}{rcl} 2\,x \, - \, 2\, (3 \, + \, x ) & = & 8                                        \\
−
</div> <!-- tolv5 -->
+
                            2\,x \, - \, 6 \, - \, 2\,x & = & 8                                        \\
 +
                                                  - \, 6 & = & 8 \quad {\color{Red} {\rm{Motsägelse!}}} \\
 +
                                                        & \Downarrow &
 +
      \end{array}</math>
  
 +
<math> \qquad\quad </math> Ekvationen saknar lösning.
  
−
<div class="exempel"> <!-- exempel5 -->
+
</div>
−
== <b><span style="color:#931136">Varför är <math> \; 5 \cdot 0 \, = \, 0 \; </math>?</span></b> ==
+
−
<big>
+
  
−
::::<math> \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 </math>
 
  
−
::::<math> \;\; 5 \cdot 3 \; = \; {\color{Red} 0} + 5 + 5 + 5 </math>
+
</div>
  
−
::::<math> \;\; 5 \cdot 2 \; = \; {\color{Red} 0} + 5 + 5 </math>
 
  
−
::::<math> \;\; 5 \cdot 1 \; = \; {\color{Red} 0} + 5 </math>
+
== <b><span style="color:#931136">När är alla tal lösningar till en ekvation?</span></b> ==
  
−
::::<math> \;\; {\color{Red} {5 \cdot 0 \; = \; 0}} </math>
+
<br>
  
−
::::<math> \;\; 5 \cdot (-1) \; = \; {\color{Red} 0} - 5 </math>
+
<div class="ovnA">
 +
<big><b><span style="color:#931136">Exempel:</span></b></big>
  
−
::::<math> \;\; 5 \cdot (-2) \; = \; {\color{Red} 0} - 5 - 5 </math>
+
<div class="exempel">
 +
<math>\begin{array}{rcl} \;\; x \, - \, (4 \, + \, x ) & = & -4                                          \\
 +
                                x \, - \, 4 \, - \, x & = & -4                                          \\
 +
                                                - \, 4 & = & -4 \quad {\color{Red} {\rm{Alltid\;sant!}}} \\
 +
                                                      & \Downarrow &
 +
      \end{array}</math>
  
−
::::<math> \;\; 5 \cdot (-3) \; = \; {\color{Red} 0} - 5 - 5 - 5 </math>
+
<math> \;\; </math> Alla tal är lösningar till ekvationen. Eller<span style="color:black">:</span>
  
−
::::<math> \;\; 5 \cdot (-4) \; = \; {\color{Red} 0} - 5 - 5 - 5 - 5 </math>
+
<math> \;\; </math> Ekvationen har oändligt många lösningar.
  
−
Att <math> \; {\color{Red} 0} </math>-orna följer med hela tiden beror på att additionens ''enhet'' är <math> \, {\color{Red} 0} </math>, dvs <math> \, a + {\color{Red} 0} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 0} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5 \cdot 0}} \, </math> då alla <math> \, 5</math>-or har försvunnit.
+
</div>
−
</big>
+
−
</div> <!-- exempel5 -->
+
  
  
−
== <b><span style="color:#931136">Internetlänkar</span></b> ==
+
</div>
−
 
+
−
https://www.youtube.com/watch?v=BMEOkzq3Xo4
+
−
 
+
−
http://www.youtube.com/watch?v=iYgG4LUqXks
+
−
 
+
−
http://www.webbmatte.se/gym/arabiska/2/2_8_4sv.html
+
−
 
+
−
http://www.webbmatte.se/gym/arabiska/2/2_8_3sv.html
+
  
  
Rad 310: Rad 278:
  
  
−
[[Matte:Copyrights|Copyright]] © 2010-2016 Math Online Sweden AB. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2021 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 15 december 2021 kl. 13.28

        <<  Förra avsnitt          Genomgång          Quiz          Övningar          Nästa avsnitt  >>      


Varför ekvationer?


Exempel på en textuppgift:

Kalle köper en flaska dryck som kostar \( \, 18 \, \) kr med pant.
Drycken (innehållet) kostar \( \, 14 \, \) kr mer än panten (flaskan).
Hur mycket kostar flaskan?

Utan ekvation svarar de flesta 4 kr, vilket är fel.

Lösning med ekvation: \( \quad\;\;\; x \; = \; {\rm flaskans\;pris} \)

\[ \qquad\qquad\;\; x \, + \, 14 \; = \; {\rm dryckens\;pris} \]
\[\begin{array}{rcl} x \, + \, (x \, + \, 14) & = & 18 \\ x \, + \, x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 & = & 18 \\ 2\,x \, & = & 4 \\ x \, & = & {\color{Red} 2} \end{array}\]


Svar:     Flaskan kostar \( \, {\color{Red} {2 \; {\rm kr\,}}}\).


För mer info om hur man ställer upp en ekvation och om lösningsmetoder se:


Metoden att ställa upp en ekvation utifrån en textuppgift,

Övertäckningsmetoden \( \quad \) och \( \quad \) Allmän metod.

\( \;\; \)
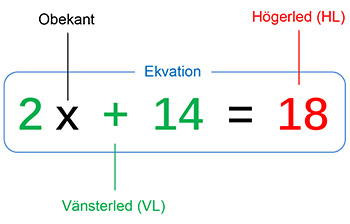
Vad är en ekvation?


\( \qquad\quad \)Ekvation Obekant VL HL 350.jpg

En ekvation är en likhet mellan två uttryck,

har alltid formen VL = HL och innehåller

minst en variabel, kallad obekant.

Ex.: \( \qquad\quad 2\,x \; + \; 14 \; = \; 18 \)

Ekvationens lösning: \( \quad\; \)
\( x \; = \; {\color{Red} 2} \)


Varför lösning?

Kontroll: Sätt in lösningen i ekvationen.

VL \( \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 \)

HL \( \, = \, 18 \)

VL \( = \) HL \( \, \implies \, x = {\color{Red} 2} \) är en lösning.

Kontroll kallas ibland även för prövning.


Om kontrollen ovan säger man: Lösningen satisfierar (uppfyller) ekvationen.


Men hur får man lösningen? Det finns två lösningsmetoder:


1.   Övertäckningsmetoden

Exemplet ovan:

  \( 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x \)

\(\quad\)
\( \, + \;\, 14 \; = \; 18 \)

  \( \;\, {\color{Red} ?} \;\;\; + \; 14 \; = \; 18 \)

  \( \;\, {\color{Red} 4} \;\;\; + \; 14 \; = \; 18 \)

  \( \;\, \Downarrow \)

  \( \, 2 \, \cdot \; x \;\; = \;\, {\color{Red} 4} \qquad\quad {\color{Red} {\rm Täck\;över\;}} x \)

  \( \, 2 \, \cdot \; \)
\( \quad \)
\( \; = \;\, 4 \)

  \( \, 2 \, \cdot \; {\color{Red} ?} \;\; = \;\; 4 \)

  \( \, 2 \, \cdot \; {\color{Red} 2} \;\; = \;\; 4 \)

  \( \quad\;\;\; \Downarrow \)

 
\( \; x \; = \; {\color{Red} 2} \)


2.   Allmän metod

Exempel:

\[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad | & {\color{Red} {- \, 14}} \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ 2 \cdot x \, & = & 4 & \qquad | & {\color{Red} {/ \; 2}} \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x \, & = & 2 & & \end{array}\]

Skrivsättet \( \quad\;\;\, | \quad {\color{Red} {- \, 14}} \quad\;\;\, \) är en kommentar och betyder:

Subtrahera \( \, 14 \, \) från ekvationens båda led.

Kommentaren \( \;\; | \quad {\color{Red} {/ \; 2}} \;\; \) betyder:

Dividera ekvationens båda led med \( \, 2 \).


Den allmänna metoden steg för steg

Steg 1

  Förenkla uttrycken i ekvationens båda led

  så långt som möjligt. I exemplet ovan:

\[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & & \end{array}\]

Steg 2

  Utför samma operation på båda leden:

\[\begin{array}{rcl} 2\,x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} \\ 2\,x \, & = & 4 \end{array}\]

Vilken operation?

Den inversa operation som isolerar \( x\)-termen.

\( \;\;\; {\color{Red} {- \, 14}} \, \) är den inversa operationen till \( \, + \, 14 \)

Steg 3

  Utför samma operation på båda leden:

\[\begin{array}{rclcl} \quad\; 2 \cdot x \, & = & 4 & & \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x & = & 2 & & \end{array}\]

Vilken operation?

Den inversa operation som isolerar \( \, x \, \).

\( \quad\;\; {\color{Red} {/ \; 2}} \, \) är den inversa operationen till \( \, \cdot \; 2 \)



Den allmänna metodens filosofi:

Betrakta ekvationen som en våg i balans.

HL och VL är vågens skålar. Likhetsteck-

net betyder att vågens skålar är i balans.

Bibehåll balansen genom att utföra:

\( \;\;\; \) Samma operation på båda leden !

Välj alltid den inversa operationen till den

operation som binder \( \, x \, \) till dess omgivning.


När saknar en ekvation lösning?


Exempel:

\(\begin{array}{rcl} 2\,x \, - \, 2\, (3 \, + \, x ) & = & 8 \\ 2\,x \, - \, 6 \, - \, 2\,x & = & 8 \\ - \, 6 & = & 8 \quad {\color{Red} {\rm{Motsägelse!}}} \\ & \Downarrow & \end{array}\)

\( \qquad\quad \) Ekvationen saknar lösning.



När är alla tal lösningar till en ekvation?


Exempel:

\(\begin{array}{rcl} \;\; x \, - \, (4 \, + \, x ) & = & -4 \\ x \, - \, 4 \, - \, x & = & -4 \\ - \, 4 & = & -4 \quad {\color{Red} {\rm{Alltid\;sant!}}} \\ & \Downarrow & \end{array}\)

\( \;\; \) Alla tal är lösningar till ekvationen. Eller:

\( \;\; \) Ekvationen har oändligt många lösningar.






Copyright © 2021 TechPages AB. All Rights Reserved.

Hämtad från "https://matte1b.mathonline.se/index.php?title=3.3_Ekvationer_2_kolumner&oldid=37413"