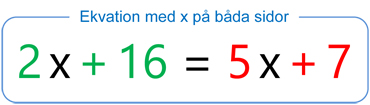Skillnad mellan versioner av "3.4 Ekvationer med x på båda sidor"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(14 mellanliggande versioner av samma användare visas inte)
Rad 6: Rad 6:
 
{{Not selected tab|[[3.4 Övningar till Ekvationer med x på båda sidor|Övningar]]}}
 
{{Not selected tab|[[3.4 Övningar till Ekvationer med x på båda sidor|Övningar]]}}
 
{{Not selected tab|[[3.4 Lathund till Ekvationer med x på båda sidor|Lathund]]}}
 
{{Not selected tab|[[3.4 Lathund till Ekvationer med x på båda sidor|Lathund]]}}
 +
{{Not selected tab|[[3.5 Potensekvationer|Nästa avsnitt  >> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"|  
 
| style="border-bottom:1px solid #797979"  width="100%"|  
 
|}
 
|}
 +
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 +
| style="border-bottom:1px solid #797979" width="5px" |  
 +
{{Not selected tab|[[3.3 Ekvationer| <<&nbsp;&nbsp;Förra avsnitt]]}}
 +
{{Not selected tab|    }}
 +
{{Not selected tab|    }}
 +
{{Not selected tab|    }}
 +
{{Not selected tab|    }}
 +
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 +
|}
 +
 +
 +
<big>Med "Ekvationer med <math> \, x \, </math> på båda sidor" menas ekvationer som har <math> \, x</math>-termer på båda sidor av likhetstecknet.
 +
</big>
 +
 +
 +
== <b><span style="color:#931136">Fall 1: &nbsp; <math> x</math>-term med större koefficient finns på VL</span></b> ==
 +
<big>Med "koefficient" menas det tal som står framför ett <math> \, x \, </math>.
 +
 +
T.ex. är 4 koefficienten till <math> x</math>-termen <math> 4\,x</math>.
 +
 +
2 är koefficienten till <math> x</math>-termen <math> 2\,x</math>.</big>
 +
 +
 +
<math> \qquad </math>[[Image: Bild Ekvation x bada sidor 370.jpg]]
 +
 +
<big><big> <math> \qquad {\bf{\color{LimeGreen} 4}} \, </math> är koefficienten till termen <math> \, 4\,x \, </math>.
 +
 +
<math> \qquad {\bf{\color{Red} 2}} \, </math> är koefficienten till termen <math> \, 2\,x </math><span style="color:black">:</span> <math> \quad {\bf{\color{LimeGreen} 4}} \, > {\bf{\color{Red} 2}} </math></big></big>
 +
<br><br>
 +
<div class="ovnE">
 +
<b>Steg 1</b>
 +
<div class="exempel">
 +
 +
&nbsp; Samla alla <math> x</math>-termer på det led vars <math> x</math>-term
 +
 +
&nbsp; har större koefficient, i exemplet ovan på <b><span style="color:red">VL</span></b><span style="color:black">:</span>
 +
 +
<math>\begin{array}{rcl} {\bf{\color{LimeGreen} 4}}\,x \, + \, 6    & = & {\bf{\color{Red} 2}}\,x \, + \, 14                \\
 +
                  \quad 4\,x \, + \, 6 \; {\color{Red} {- \; 2\,x}} & = & 2\,x \, + \, 14 \; {\color{Red} {- \; 2\,x}} \quad \\
 +
                                                      2\,x \, + \, 6 & = & 14                                     
 +
      \end{array}</math>
 +
 +
&nbsp; Detta för att undvika negativa <math> x</math>-termer.
 +
</div>
 +
 +
<b>Steg 2</b>
 +
<div class="exempel">
 +
 +
&nbsp; Samla alla konstanta termer (utan <math>x</math>) på ekva-
 +
 +
&nbsp; tionens andra led, i exemplet ovan på <b><span style="color:red">HL</span></b><span style="color:black">:</span>
 +
 +
<math>\begin{array}{rcl}                            2\,x \, + \, 6 & = & 14                          \\
 +
                  \qquad 2\,x \, + \, 6 \; {\color{Red} {- \; 6}} & = & 14 \; {\color{Red} {- \; 6}} \\
 +
                                                  2\,x \,        & = & 8                                       
 +
      \end{array}</math>
 +
</div>
 +
 +
<b>Steg 3</b>
 +
<div class="exempel">
 +
 +
&nbsp; Lös ekvationen enligt den [[3.3_Ekvationer#2._.C2.A0_Allm.C3.A4n_metod|<b><span style="color:blue">allmänna metoden</span></b>]]<span style="color:black">:</span>
 +
 +
<math>\begin{array}{rcl}                                          2 \cdot x \,        & = & 8                                        \\
 +
                  \qquad\qquad\quad \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{8}{{\color{Red} {2}}} \\
 +
                                                                          x \,        & = & 4                                             
 +
      \end{array}</math>
 +
</div>
 +
 +
 +
</div>
 +
 +
 +
== <b><span style="color:#931136">Fall 2: &nbsp; <math> x</math>-term med större koefficient finns på HL</span></b> ==
 +
<br><br>
 +
<math> \qquad </math>[[Image: Bild Ekvation x bada sidor Fall 2 370a.jpg]]
 +
 +
 +
<big><big> <math> \qquad {\bf{\color{Red} 5}} \, </math> är koefficienten till termen <math> \, 5\,x \, </math>.
 +
 +
<math> \qquad {\bf{\color{LimeGreen} 2}} \, </math> är koefficienten till termen <math> \, 2\,x </math><span style="color:black">:</span> <math> \quad {\bf{\color{Red} 5}} \, > {\bf{\color{LimeGreen} 2}} </math></big></big>
 +
<br><br>
 +
<div class="ovnE">
 +
<b>Steg 1</b>
 +
<div class="exempel">
 +
 +
&nbsp; Samla alla <math> x</math>-termer på det led vars <math> x</math>-term har
 +
 +
&nbsp; större koefficient, i fall 2 på <b><span style="color:red">HL</span></b><span style="color:black">:</span>
 +
 +
<math>\begin{array}{rcl} {\bf{\color{LimeGreen} 2}} \,x \, + \, 16    & = & {\bf{\color{Red} 5}} \,x \, + \, 7                \\
 +
                  \quad 2\,x \, + \, 16 \; {\color{Red} {- \; 2\,x}} & = & 5\,x \, + \, 7 \; {\color{Red} {- \; 2\,x}} \quad \\
 +
                                                                  16 & = & 3\,x \, + \, 7                                     
 +
      \end{array}</math>
 +
 +
&nbsp; Detta för att undvika negativa <math> x</math>-termer.
 +
</div>
 +
 +
<b>Steg 2</b>
 +
<div class="exempel">
 +
 +
&nbsp; Samla alla konstanta termer (utan <math>x</math>) på ekva-
 +
 +
&nbsp; tionens andra led, i fall 2 på <b><span style="color:red">VL</span></b><span style="color:black">:</span>
 +
 +
<math>\begin{array}{rcl}                                16 & = & 3\,x \, + \, 7                          \\
 +
                  \qquad\quad 16 \; {\color{Red} {- \; 7}} & = & 3\,x \, + \, 7 \; {\color{Red} {- \; 7}} \\
 +
                                                      9 \, & = & 3\,x                                       
 +
      \end{array}</math>
 +
</div>
 +
 +
<b>Steg 3</b>
 +
<div class="exempel">
 +
 +
&nbsp; Lös ekvationen enligt den [[3.3_Ekvationer#2._.C2.A0_Allm.C3.A4n_metod|<b><span style="color:blue">allmänna metoden</span></b>]]<span style="color:black">:</span>
 +
 +
<math>\begin{array}{rcl}                                                  9 \, & = & 3 \cdot x                                        \\
 +
                  \qquad\qquad\quad \displaystyle \frac{9}{{\color{Red} {3}}} & = & \displaystyle \frac{3 \cdot x}{{\color{Red} {3}}} \\
 +
                                                                          3 \, & = & x                                                \\
 +
                                                                          x \, & = & 3
 +
      \end{array}</math>
 +
</div>
 +
 +
 +
</div>
 +
 +
 +
<div class="border-divblue">
 +
<big>
 +
<b><span style="color:#931136">Fall 2:s filosofi:</span></b>
 +
 +
Lösningsmetoden i fall 2 är en rekommen-
 +
 +
dation som gör beräkningen <b><span style="color:red">effektivare</span></b>:
 +
 +
Man undviker hanteringen av negativa <math> x</math>-
 +
 +
termer och minustecknet, vilket
 +
 +
<math> \quad\;\;\; </math> <b><span style="color:red">minskar risken för felräkning.</span></b>
 +
</big></div>
 +
 +
 +
== <b><span style="color:#931136">När har en ekvation ingen lösning alls?</span></b> ==
 +
 +
<br>
 +
 +
<div class="ovnC">
 +
<big><b><span style="color:#931136">Exempel:</span></b></big>
 +
 +
<div class="exempel">
 +
<math>\begin{array}{rcl}      3 \, (5 \, + \, x) & = & 3\,x \, + \, 18                              \\
 +
                                  15 \, + \, 3\,x & = & 3\,x \, + \, 18                              \\
 +
\;\; 15 \, + \, 3\,x \, {\color{Red} {- \, 3\,x}} & = & 3\,x \, + \, 18 \, {\color{Red} {- \, 3\,x}} \\
 +
                                              15  & = & 18 \quad {\color{Red} {\rm{Motsägelse!}}}    \\
 +
                                                  & \Downarrow &
 +
      \end{array}</math>
 +
 +
<math> \;\; </math> Ekvationen har ingen lösning alls. Kort<span style="color:black">:</span>
 +
 +
<math> \qquad\quad </math> Ekvationen saknar lösning.
 +
 +
</div>
 +
 +
 +
</div>
 +
 +
 +
== <b><span style="color:#931136">När har en ekvation oändligt många lösningar?</span></b> ==
 +
 +
<br>
 +
 +
<div class="ovnA">
 +
<big><b><span style="color:#931136">Exempel:</span></b></big>
 +
 +
<div class="exempel">
 +
<math>\begin{array}{rcl}      3 \, (5 \, + \, x) & = & 3\,x \, + \, 15                              \\
 +
                                  15 \, + \, 3\,x & = & 3\,x \, + \, 15                              \\
 +
\;\; 15 \, + \, 3\,x \, {\color{Red} {- \, 3\,x}} & = & 3\,x \, + \, 15 \, {\color{Red} {- \, 3\,x}} \\
 +
                                              15  & = & 15 \quad {\color{Red} {\rm{Alltid\;sant!}}}    \\
 +
                                                  & \Downarrow &
 +
      \end{array}</math>
 +
 +
<math> \;\; </math> Alla tal är lösningar till ekvationen. Eller<span style="color:black">:</span>
 +
 +
<math> \;\; </math> Ekvationen har oändligt många lösningar.
 +
 +
</div>
 +
 +
 +
</div>
 +
 +
 +
  
  
−
Med "Ekvationer med <math> \, x \, </math> på båda sidor" menas Ekvationer med <math> \, x</math>-termer på båda sidor av likhetstecknet.
 
  
  
Rad 16: Rad 210:
  
  
−
[[Matte:Copyrights|Copyright]] © 2010-2017 Math Online Sweden AB. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2022 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 13 januari 2022 kl. 10.41

       Genomgång          Quiz          Övningar          Lathund          Nästa avsnitt  >>      
        <<  Förra avsnitt                                              


Med "Ekvationer med \( \, x \, \) på båda sidor" menas ekvationer som har \( \, x\)-termer på båda sidor av likhetstecknet.


Fall 1:   \( x\)-term med större koefficient finns på VL

Med "koefficient" menas det tal som står framför ett \( \, x \, \).

T.ex. är 4 koefficienten till \( x\)-termen \( 4\,x\).

2 är koefficienten till \( x\)-termen \( 2\,x\).


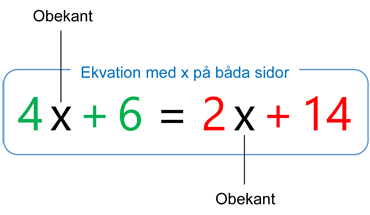
\( \qquad \)Bild Ekvation x bada sidor 370.jpg

\( \qquad {\bf{\color{LimeGreen} 4}} \, \) är koefficienten till termen \( \, 4\,x \, \).

\( \qquad {\bf{\color{Red} 2}} \, \) är koefficienten till termen \( \, 2\,x \): \( \quad {\bf{\color{LimeGreen} 4}} \, > {\bf{\color{Red} 2}} \)

Steg 1

  Samla alla \( x\)-termer på det led vars \( x\)-term

  har större koefficient, i exemplet ovan på VL:

\(\begin{array}{rcl} {\bf{\color{LimeGreen} 4}}\,x \, + \, 6 & = & {\bf{\color{Red} 2}}\,x \, + \, 14 \\ \quad 4\,x \, + \, 6 \; {\color{Red} {- \; 2\,x}} & = & 2\,x \, + \, 14 \; {\color{Red} {- \; 2\,x}} \quad \\ 2\,x \, + \, 6 & = & 14 \end{array}\)

  Detta för att undvika negativa \( x\)-termer.

Steg 2

  Samla alla konstanta termer (utan \(x\)) på ekva-

  tionens andra led, i exemplet ovan på HL:

\(\begin{array}{rcl} 2\,x \, + \, 6 & = & 14 \\ \qquad 2\,x \, + \, 6 \; {\color{Red} {- \; 6}} & = & 14 \; {\color{Red} {- \; 6}} \\ 2\,x \, & = & 8 \end{array}\)

Steg 3

  Lös ekvationen enligt den allmänna metoden:

\(\begin{array}{rcl} 2 \cdot x \, & = & 8 \\ \qquad\qquad\quad \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{8}{{\color{Red} {2}}} \\ x \, & = & 4 \end{array}\)



Fall 2:   \( x\)-term med större koefficient finns på HL



\( \qquad \)Bild Ekvation x bada sidor Fall 2 370a.jpg


\( \qquad {\bf{\color{Red} 5}} \, \) är koefficienten till termen \( \, 5\,x \, \).

\( \qquad {\bf{\color{LimeGreen} 2}} \, \) är koefficienten till termen \( \, 2\,x \): \( \quad {\bf{\color{Red} 5}} \, > {\bf{\color{LimeGreen} 2}} \)

Steg 1

  Samla alla \( x\)-termer på det led vars \( x\)-term har

  större koefficient, i fall 2 på HL:

\(\begin{array}{rcl} {\bf{\color{LimeGreen} 2}} \,x \, + \, 16 & = & {\bf{\color{Red} 5}} \,x \, + \, 7 \\ \quad 2\,x \, + \, 16 \; {\color{Red} {- \; 2\,x}} & = & 5\,x \, + \, 7 \; {\color{Red} {- \; 2\,x}} \quad \\ 16 & = & 3\,x \, + \, 7 \end{array}\)

  Detta för att undvika negativa \( x\)-termer.

Steg 2

  Samla alla konstanta termer (utan \(x\)) på ekva-

  tionens andra led, i fall 2 på VL:

\(\begin{array}{rcl} 16 & = & 3\,x \, + \, 7 \\ \qquad\quad 16 \; {\color{Red} {- \; 7}} & = & 3\,x \, + \, 7 \; {\color{Red} {- \; 7}} \\ 9 \, & = & 3\,x \end{array}\)

Steg 3

  Lös ekvationen enligt den allmänna metoden:

\(\begin{array}{rcl} 9 \, & = & 3 \cdot x \\ \qquad\qquad\quad \displaystyle \frac{9}{{\color{Red} {3}}} & = & \displaystyle \frac{3 \cdot x}{{\color{Red} {3}}} \\ 3 \, & = & x \\ x \, & = & 3 \end{array}\)



Fall 2:s filosofi:

Lösningsmetoden i fall 2 är en rekommen-

dation som gör beräkningen effektivare:

Man undviker hanteringen av negativa \( x\)-

termer och minustecknet, vilket

\( \quad\;\;\; \) minskar risken för felräkning.


När har en ekvation ingen lösning alls?


Exempel:

\(\begin{array}{rcl} 3 \, (5 \, + \, x) & = & 3\,x \, + \, 18 \\ 15 \, + \, 3\,x & = & 3\,x \, + \, 18 \\ \;\; 15 \, + \, 3\,x \, {\color{Red} {- \, 3\,x}} & = & 3\,x \, + \, 18 \, {\color{Red} {- \, 3\,x}} \\ 15 & = & 18 \quad {\color{Red} {\rm{Motsägelse!}}} \\ & \Downarrow & \end{array}\)

\( \;\; \) Ekvationen har ingen lösning alls. Kort:

\( \qquad\quad \) Ekvationen saknar lösning.



När har en ekvation oändligt många lösningar?


Exempel:

\(\begin{array}{rcl} 3 \, (5 \, + \, x) & = & 3\,x \, + \, 15 \\ 15 \, + \, 3\,x & = & 3\,x \, + \, 15 \\ \;\; 15 \, + \, 3\,x \, {\color{Red} {- \, 3\,x}} & = & 3\,x \, + \, 15 \, {\color{Red} {- \, 3\,x}} \\ 15 & = & 15 \quad {\color{Red} {\rm{Alltid\;sant!}}} \\ & \Downarrow & \end{array}\)

\( \;\; \) Alla tal är lösningar till ekvationen. Eller:

\( \;\; \) Ekvationen har oändligt många lösningar.







Copyright © 2022 TechPages AB. All Rights Reserved.

Hämtad från "https://matte1b.mathonline.se/index.php?title=3.4_Ekvationer_med_x_på_båda_sidor&oldid=37447"