Nuvarande version från 11 januari 2023 kl. 19.53

Genomgång

\( \qquad\qquad \)

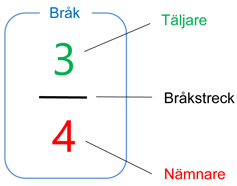
Bråkstrecket betyder division:

\( \quad\; \displaystyle \frac{{\color{Limegreen} 3}}{{\color{Red} 4}} \; = \; {\color{Limegreen} 3} \, / \, {\color{Red} 4} \; = \; 0,75 \)

Generellt

Alla tal i bråkform kan skrivas i decimalform,

men inte tvärtom.

Ex.:

\(\frac{1}{3}\) är ett tal i bråkform som kan skrivas i decimalform: \(0,333\ldots\)

Men \(\sqrt{2} = 1,414213\ldots\) kan inte anges i bråkform, eftersom:

\(\sqrt{2}\) har en oändlig icke-periodisk decimalutveckling.

\(\sqrt{2}\;\) är ett exempel på ett irrationellt tal, se Olika typer av tal.

Tal i bråkform är synonym till rationella tal.

Heltal som bråk

\( \qquad \displaystyle 9 \; = \; \frac{9}{1} \qquad \)

Generellt

Alla heltal kan skrivas i bråkform med nämnaren \( {\color{Red} 1} \, \).

Slutsats: Alla heltal är även rationella tal, dvs

Mängden av alla heltal är delmängd i mängden

av alla rationella tal, se Lökmodellen.

Blandad form

Bråk vars täljare > nämnare kan skrivas i blandad form.

Omvandling av bråk till blandad form

Skriv \( \; \frac{7}{2} \; \) i blandad form:

\( \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \; \color {Limegreen} 3 \,, {\rm rest} \; 1 \; = \; \boxed{\color {Limegreen} 3 \,\frac{1}{\color {Red} 2}} \quad \)

\( \quad \) Eller använd miniräknare:

\( \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \quad\; 3,5 \quad\; = \; \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \quad \)

Omvandling av blandad form till bråk

Skriv den blandade formen till bråk:

\( \quad \displaystyle \boxed{\color {Limegreen} 3\,\frac{1}{\color {Red} 2}} \;\; = \;\; \frac{\color {Limegreen} 3 \, \cdot \color {Red} 2 \quad + \quad 1}{\color {Red} 2} \;\; = \;\; \frac{7}{\color {Red} 2} \)

\( \quad \) Därför att:

\( \quad \displaystyle \color {Limegreen} 3\,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \; + \; \frac{1}{\color {Red} 2} = \frac{\color {Limegreen} 3}{1} + \frac{1}{\color {Red} 2} \; = \)

\( \qquad\;\;\, \displaystyle \; = \; \frac{\color {Limegreen} 3 \cdot \color {Red} 2}{1 \cdot \color {Red} 2} \; + \; \frac{1}{\color {Red} 2} \; = \; \frac{6}{\color{Red} 2} \; + \; \frac{1}{\color{Red} 2} \; = \; \frac{7}{\color{Red} 2} \)

Regeln

\( \quad \displaystyle \color {Limegreen} a\;\frac{b}{\color {Red} c} \quad = \quad \frac{\color {Limegreen} a \, \cdot \color {Red} c \quad + \quad b}{\color {Red} c} \quad \)

Förklaring för \( \; + \; \) i de två rutorna ovan

I blandade former står mellan heltalet och

bråket ett osynligt + \( \quad \displaystyle \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \) + \( \displaystyle \frac{1}{\color {Red} 2} \quad \)

Läs därför: "Tre och en halv"

Förkortning av bråk

Förkorta bråken så långt som möjligt:

1) \( \quad \displaystyle \frac{2}{4} \; = \; \frac{1 \cdot 2}{2 \cdot 2} \; = \; \frac{1 \cdot \cancel{\color{Red} 2}}{2 \cdot \cancel{\color{Red} 2}} \; = \; \frac{1}{2} \)

2) \( \quad \displaystyle \frac{6}{9} \; = \; \frac{2 \cdot 3}{3 \cdot 3} \; = \; \frac{2 \cdot \cancel{\color{Red} 3}}{3 \cdot \cancel{\color{Red} 3}} \; = \; \frac{2}{3} \)

3) \( \quad \displaystyle \frac{10}{15} \; = \; \frac{2 \cdot 5}{3 \cdot 5} \; = \; \; \frac{2 \cdot \cancel{\color{Red} 5}}{3 \cdot \cancel{\color{Red} 5}} \; = \; \frac{2}{3} \)

4) \( \quad \displaystyle \frac{8}{24} \; = \; \frac{\cancel{\color{Red} 2} \cdot 4}{\cancel{\color{Red} 2} \cdot 12} \, = \, \frac{\cancel{\color{Red} 2} \cdot 2}{\cancel{\color{Red} 2} \cdot 6} \, = \, \frac{\cancel{\color{Red} 2} \cdot 1}{\cancel{\color{Red} 2} \cdot 3} \, = \, \frac{1}{3} \)

Metoden:

Hitta en gemensam faktor hos täljaren och nämna-

ren. Dividera både täljaren och nämnaren med

samma gemensamma faktor.

Rekommendation

Förkorta alltid ett bråk när det är möjligt för att få

mindre tal och därmed minska risken för felräknning.

Förlängning av bråk

Förläng bråken:

1) \( \quad \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 3}}{4 \cdot {\color{Red} 3}} \; = \; \frac{9}{12} \)

2) \( \quad \displaystyle \frac{2}{3} \; = \; \frac{2 \cdot {\color{Red} 4}}{3 \cdot {\color{Red} 4}} \; = \; \frac{8}{12} \)

3) \( \quad \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 5}}{4 \cdot {\color{Red} 5}} \; = \; \frac{15}{20} \; = \; \frac{15 \cdot {\color{Red} 5}}{20 \cdot {\color{Red} 5}} \; = \; \frac{75}{100} \)

4) \( \quad \displaystyle {1 \over 8} \; = \; {1 \cdot {\color{Red} 5} \over 8 \cdot {\color{Red} 5}} \; = \; {5 \over 40} \; = \; {5 \cdot {\color{Red} 5} \over 40 \cdot {\color{Red} 5}} \; = \; {25 \over 200} \; = \)

\( \qquad\quad\; \displaystyle = \; {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \; = \; {125 \over 1\,000} \)

Metoden:

Multiplicera täljaren och nämnaren med samma tal.

Slutsats

Både förkortning och förlängning bibehåller

bråkets värde.

När ska man förlänga bråk?

1) Jämförelse av bråk:

Ex.: Vilket av bråken är större: \( \quad \displaystyle \frac{3}{4} \quad \) eller \( \quad \displaystyle \frac{2}{3} \quad \) ?

Det kan man bara avgöra genom att förlänga dem till sam-

ma nämnare, se Förlängnng av bråk, ex. 1 och 2:

\( \qquad\;\; \displaystyle \frac{9}{12} \, > \, \frac{8}{12} \qquad \implies \qquad\displaystyle \frac{3}{4} \, > \, \frac{2}{3} \)

2) Addition av bråk med olika nämnare:

Se nedan: Fall 2 Bråk med olika nämnare.

Addition och subtraktion av bråk

Fall 1 Bråk med samma nämnare

\( \quad \displaystyle \frac{1}{\color{Red} 5} \; + \; \frac{3}{\color{Red} 5} \; = \; \frac{4}{\color{Red} 5} \)

\( \quad \displaystyle \frac{11}{\color{Red} {12}} \; - \; \frac{5}{\color{Red} {12}} \; = \; \frac{6}{\color{Red} {12}} \; = \; \frac{1 \cdot \cancel{6}}{2 \cdot \cancel{6}} \; = \; \frac{1}{2} \)

\( \quad \displaystyle \frac{5}{\color{Red} {11}} + \frac{13}{\color{Red} {11}} - \frac{9}{\color{Red} {11}} = \frac{5+13-9}{\color{Red} {11}} = \frac{9}{\color{Red} {11}} \quad \)

Regeln för add./subtr. av bråk med samma nämnare

Bibehåll och ta över den gemensamma

nämnaren. Addera/subtrahera täljarna.

Fall 2 Bråk med olika nämnare

\( \quad \displaystyle \frac{1}{2} \; + \; \frac{1}{3} \; = \; \frac{1 \cdot {\color{Limegreen} 3}}{2 \cdot {\color{Limegreen} 3}} \; + \; \frac{1 \cdot {\color{Limegreen} 2}}{3 \cdot {\color{Limegreen} 2}} \; = \; \)

\( \qquad\qquad\;\; \displaystyle \; = \; \frac{3}{\color{Red} 6} \; + \; \frac{2}{\color{Red} 6} \; = \; \frac{5}{\color{Red} 6} \)

\( \quad \displaystyle \frac{2}{3} \; + \; \frac{1}{5} \; = \; \frac{2 \cdot {\color{Limegreen} 5}}{3 \cdot {\color{Limegreen} 5}} \; + \; \frac{1 \cdot {\color{Limegreen} 3}}{5 \cdot {\color{Limegreen} 3}} \; = \; \)

\( \qquad\qquad\;\; \displaystyle \; = \; \frac{10}{\color{Red} {15}} \; + \; \frac{3}{\color{Red} {15}} \; = \; \frac{13}{\color{Red} {15}} \)

\( \quad \displaystyle \frac{7}{4} \; - \; \frac{5}{3} \; = \; \frac{7 \cdot {\color{Limegreen} 3}}{4 \cdot {\color{Limegreen} 3}} \; - \; \frac{5 \cdot {\color{Limegreen} 4}}{3 \cdot {\color{Limegreen} 4}} \; = \; \)

\( \qquad\qquad\;\; \displaystyle \; = \; \frac{21}{\color{Red} {12}} \; - \; \frac{20}{\color{Red} {12}} \; = \; \frac{1}{\color{Red} {12}} \quad \)

Produktmetoden för add./subtr. av bråk med olika nämnare

1) Förläng bråken så att de får en gemen-

sam nämnare ( = nämnarnas produkt).

2) Ta över den gemensamma nämnaren.

Addera/subtrahera täljarna.

En bättre metod:

Minsta gemensamma nämnare (MGN)

Produktmetoden:

\( \quad \displaystyle \frac{1}{6} \; + \; \frac{2}{9} \; = \; \frac{1 \cdot {\color{Limegreen} 9}}{6 \cdot {\color{Limegreen} 9}} \; + \; \frac{2 \cdot {\color{Limegreen} 6}}{9 \cdot {\color{Limegreen} 6}} \; = \; \)

\( \quad \displaystyle \, = \, \frac{9}{\color{Red} {54}} \, + \, \frac{12}{\color{Red} {54}} \, = \, \frac{21}{\color{Red} {54}} \, = \, \frac{7 \cdot \cancel{\color{Red} 3}}{18 \cdot \cancel{\color{Red} 3}} \, = \, \frac{7}{18} \)

Produktmetoden hittar en gemensam nämnare: 54.

MGN-metoden:

\( \quad \displaystyle \frac{1}{6} \; + \; \frac{2}{9} \; = \; \frac{1}{2 \cdot {\color{Red} 3}} \; + \; \frac{2}{3 \cdot {\color{Red} 3}} \; = \; \)

\( \quad \displaystyle \, = \, \frac{1 \cdot {\color{Limegreen} 3}}{6 \cdot {\color{Limegreen} 3}} \; + \; \frac{2 \cdot {\color{Limegreen} 2}}{9 \cdot {\color{Limegreen} 2}} \, = \, \frac{3}{\color{Red} {18}} \, + \, \frac{4}{18} \, = \, \frac{7}{18} \)

MGN-metoden hittar den minsta gem. nämnaren: 18.

Generellt

MGN = Produkt / Största gemensamma delare.

Ex.: 54 / 3 = 18.

Multiplikation av bråk

\( \quad \displaystyle \frac{1}{2} \; \cdot \; \frac{3}{4} \; = \; \frac{1 \cdot 3}{2 \cdot 4} \; = \; \frac{3}{8}\)

\( \quad \displaystyle \frac{2}{3} \; \cdot \; \frac{4}{7} \; = \; \frac{2 \cdot 4}{3 \cdot 7} \; = \; \frac{8}{21} \)

\( \quad \displaystyle \frac{3}{4} \; \cdot \; \frac{2}{3} \; = \; \frac{3 \cdot 2}{4 \cdot 3} \; = \; \frac{6}{12} \; = \; \frac{1 \cdot \cancel{6}}{2 \cdot \cancel{6}} \; = \; \frac{1}{2} \)

Regeln för multiplikation av bråk

Multiplicera:	täljarna	med	varandra,
	nämnarna	med	varandra.

Allmän regel för redovisning av bråkuppgifter

Förkorta dina svar så långt som möjligt.

Division av bråk

\( \quad \displaystyle \frac{1}{2} \; \Big/ \; \frac{3}{4} \; = \; \frac{1}{2} \; {\color{Red} {\cdot \; \frac{4}{3}}} \; = \; \frac{1 \cdot 4}{2 \cdot 3} \; = \; \frac{4}{6} \; = \; \)

\( \qquad\qquad\; \displaystyle \; = \; \frac{\cancel{2} \cdot 2}{\cancel{2} \cdot 3} \; = \; \frac{2}{3} \)

\( \quad \displaystyle \frac{2}{3} \; \Big/ \; \frac{5}{7} \; = \; \frac{2}{3} \; {\color{Red} {\cdot \; \frac{7}{5}}} \; = \; \frac{2 \cdot 7}{3 \cdot 5} \; = \; \frac{14}{15} \)

\( \quad \displaystyle \frac{4}{7} \; \Big/ \; \frac{3}{5} \; = \; \frac{4}{7} \; {\color{Red} {\cdot \; \frac{5}{3}}} \; = \; \frac{4 \cdot 5}{7 \cdot 3} \; = \; \frac{20}{21} \)

Regeln för division av bråk

Ersätt \( / \) med \( {\color{Red} {\cdot}} \) och invertera det bråk som

man skulle dividera med (dvs det andra).

Använd regeln för multiplikation av bråk.

Att invertera t.ex. \( \, \displaystyle \frac{3}{4} \, \) ger \( \, \displaystyle {\color{Red} {\frac{4}{3}}} \; \).

Dubbelbråk

\( \;\; \displaystyle \frac{\frac{{\color{Red} 2}}{{\color{Limegreen} 5}}}{\frac{{\color{Limegreen} 4}}{{\color{Red} 9}}} \) \( \displaystyle \; = \; \frac{{\color{Red} 2} \cdot {\color{Red} 9}}{{\color{Limegreen} 5} \cdot {\color{Limegreen} 4}} \; = \; \frac{\cancel{2} \cdot 9}{5 \cdot 2 \cdot \cancel{2}} \; = \; \frac{9}{5 \cdot 2} \; = \; \frac{9}{10} \)

\( \;\; \) Förkorta även på vägen till svaret om möjligt.

Regeln för dubbelbråk

Ta de "yttersta" (\( \, {\color{Red} 2} \, \) och \( \, {\color{Red} 9} \, \)) till täljaren.

Ta de "innersta" (\( \, {\color{Limegreen} 5} \, \) och \( \, {\color{Limegreen} 4} \, \)) till nämnaren.

Bråk gånger heltal

\( \displaystyle \frac{2}{3} \cdot 9 \; = \; \frac{2}{3} \cdot \frac{9}{1} \; = \; \frac{2 \cdot 9}{3 \cdot 1} \; = \; \frac{2 \cdot 3 \cdot \cancel{3}}{\cancel{3}} \; = \; 6 \)

Snabbare:

\( \displaystyle \frac{2}{3} \cdot 9 \; = \; \frac{2 \cdot 9}{3} \; = \; \frac{18}{3} \; = \; 6 \)

\( \displaystyle 2 \cdot \frac{5}{7} \; = \; \frac{2 \cdot 5}{7} \; = \; \frac{10}{7} \)

Regel

Ta täljaren \( \times \) heltalet, bibehåll nämnaren.

Bråkdel av ett tal

Bestäm \( \; \displaystyle \frac{5}{6} \; \) av \( \; 12 \; \).

\( \quad \displaystyle \frac{5}{6} \; \) \( {\color {Red} {\cdot}} \) \( \; \displaystyle 12 \; = \; \frac{5 \cdot 12}{6} \; = \; \frac{5 \cdot 2 \cdot \cancel{6}}{\cancel{6}} \; = \; 10 \quad \)

Regel

Översätt av till gånger.

Bestäm \( \; \displaystyle \frac{4}{5} \; \) av \( \; \displaystyle \frac{7}{8} \; \).

\( \quad \displaystyle \frac{4}{5} \; \) \( {\color {Red} {\cdot}} \) \( \; \displaystyle \frac{7}{8} \; = \; \frac{4 \cdot 7}{5 \cdot 8} \; = \; \frac{\cancel{4} \cdot 7}{5 \cdot 2 \cdot \cancel{4}} \; = \; \frac{7}{10} \quad \)

Skillnad mellan versioner av "1.5 Tal i bråkform"

Nuvarande version från 11 januari 2023 kl. 19.53

Heltal som bråk

Blandad form

Förkortning av bråk

Förlängning av bråk

När ska man förlänga bråk?

Addition och subtraktion av bråk

En bättre metod:

Minsta gemensamma nämnare (MGN)

Multiplikation av bråk

Division av bråk

Dubbelbråk

Bråk gånger heltal

Bråkdel av ett tal

Navigeringsmeny

Personliga verktyg

Matematik 1b

Sök

@@ Rad 4: / Rad 4: @@
 {{Not selected tab|[[1.4 Negativa tal| <<&nbsp;&nbsp;Förra avsnitt]]}}
 {{Selected tab|[[1.5 Tal i bråkform|Genomgång]]}}
-{{Not selected tab|[[1.5 Quiz till Tal i bråkform|Quiz]]}}
+<!-- {{Not selected tab|[[1.5 Lathund till Bråkräkning|Lathund]]}} -->
-{{Not selected tab|[[1.5 Övningar till Tal i bråkform|Övningar]]}}
+<!-- {{Not selected tab|[[1.5 Quiz i bråkräkning|Quiz]]}} -->
-{{Not selected tab|[[1.5 Lathund till Tal i bråkform|Lathund]]}}
+{{Not selected tab|[[1.5 Övningar i bråkräkning|Övningar]]}}
-| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
+{{Not selected tab|[[1.5 Svårare övningar i bråk|Svårare övningar]]}}
-|}
-{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
-| style="border-bottom:1px solid #797979" width="5px" | &nbsp;
-{{Not selected tab|     }}
-{{Not selected tab|     }}
-{{Not selected tab|     }}
-{{Not selected tab|     }}
 {{Not selected tab|[[1.6 Delbarhet, primtal och faktorisering|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 | style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 |}
+<br>
-<math> \qquad\quad </math><div class="ovnE">
+<math> \qquad\qquad </math><div class="ovnE">
 [[Image: Bild Tal i brakform 30.jpg]]
@@ Rad 28: / Rad 22: @@
 </div>
+<big>
+Generellt
+<div class="border-divblue">
+Alla tal i bråkform kan skrivas i decimalform,
-== <b><span style="color:#931136">Förkortning av bråk</span></b> ==
+men inte tvärtom.
-<br><div class="ovnC">
+</div>
-<big>Förkorta bråken så långt som möjligt:</big>
+</big>
-<math> \quad \displaystyle \frac{2}{4} \; = \; \frac{1 \cdot 2}{2 \cdot 2} \; = \; \frac{1 \cdot \cancel{\color{Red} 2}}{2 \cdot \cancel{\color{Red} 2}}  \; = \; \frac{1}{2} </math>
+Ex.:
+<big>
-<math> \quad \displaystyle \frac{6}{9} \; = \; \frac{2 \cdot 3}{3 \cdot 3} \; = \; \frac{2 \cdot \cancel{\color{Red} 3}}{3 \cdot \cancel{\color{Red} 3}}  \; = \; \frac{2}{3} </math>
+<math>\frac{1}{3}</math> är ett tal i bråkform som kan skrivas i decimalform<span>:</span> <math>0,333\ldots</math>
-<math> \quad \displaystyle \frac{10}{15} \; = \; \frac{2 \cdot 5}{3 \cdot 5} \; = \; \; \frac{2 \cdot \cancel{\color{Red} 5}}{3 \cdot \cancel{\color{Red} 5}} \; = \; \frac{2}{3} </math>
+Men <math>\sqrt{2} = 1,414213\ldots</math> kan inte anges i bråkform, eftersom<span>:</span>
-<math> \quad \displaystyle \frac{8}{24} \; = \; \frac{\cancel{\color{Red} 2} \cdot 4}{\cancel{\color{Red} 2} \cdot 12} \, = \, \frac{\cancel{\color{Red} 2} \cdot 2}{\cancel{\color{Red} 2} \cdot 6} \, = \, \frac{\cancel{\color{Red} 2} \cdot 1}{\cancel{\color{Red} 2} \cdot 3} \, = \, \frac{1}{3} </math>
+<math>\sqrt{2}</math> har en <b><span style="color:red">oändlig</span></b> [[1.3_Tal_i_decimalform#Icke-periodisk_decimalutveckling|<b><span style="color:blue">icke-periodisk decimalutveckling</span></b>]].
-<b>Metoden:</b>
+<math>\sqrt{2}\;</math> är  ett exempel på ett <b><span style="color:red">irrationellt tal</span></b>, se [[1.1_Om_tal#Olika_typer_av_tal|<b><span style="color:blue">Olika typer av tal</span></b>]].
-Hitta en gemensam [[1.1_Om_tal#Summa_.5C.28-.5C.29_Differens_.5C.28-.5C.29_Produkt_.5C.28-.5C.29_Kvot|<b><span style="color:blue">faktor</span></b>]] hos täljaren och nämna-
+Tal i bråkform är synonym till <b><span style="color:red">rationella tal</span></b>.
+</big>
-ren. <b><span style="color:red">Dividera</span></b> både täljaren och nämnaren med
-samma gemensamma faktor.
+= <b><span style="color:#931136">Heltal som bråk</span></b> =
+<div class="ovnE">
+<big><math> \qquad \displaystyle  9 \; = \; \frac{9}{1} \qquad </math></big>
 </div>
-== <b><span style="color:#931136">Förlängning av bråk</span></b> ==
+<big>
+Generellt
+<div class="border-divblue">
+Alla heltal kan skrivas i bråkform med nämnaren <math> {\color{Red} 1} \, </math>.
+Slutsats: Alla heltal är även rationella tal, dvs
+Mängden av alla heltal är <b>delmängd</b> i mängden
+av alla rationella tal, se [[1.1_Om_tal#Olika_typer_av_tal|<b><span style="color:blue">Lökmodellen</span></b>]].
+</div>
+</big>
+= <b><span style="color:#931136">Blandad form</span></b> =
 <br>
 <div class="ovnA">
-<big>Förläng bråken:</big>
+<big>Bråk vars täljare > nämnare kan skrivas i blandad form.</big>
+</div>
-<b>1)</b> <math> \;\; \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 3}}{4 \cdot {\color{Red} 3}}  \; = \; \frac{9}{12} </math>
-<b>2)</b> <math> \;\; \displaystyle \frac{2}{3} \; = \; \frac{2 \cdot {\color{Red} 4}}{3 \cdot {\color{Red} 4}}  \; = \; \frac{8}{12} </math>
+<big>
+<b><span style="color:#931136">Omvandling av bråk till blandad form</span></b>
+</big>
+<div class="ovnC">
+<big>Skriv <math> \; \frac{7}{2} \; </math> i blandad form:</big>
-<b>3)</b> <math> \;\; \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 5}}{4 \cdot {\color{Red} 5}} \; = \; \frac{15}{20} \; = \; \frac{15 \cdot {\color{Red} 5}}{20 \cdot {\color{Red} 5}} \; = \; \frac{75}{100} </math>
+<math> \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \; \color {Limegreen} 3 \,, {\rm rest} \; 1 \; = \; \boxed{\color {Limegreen} 3 \,\frac{1}{\color {Red} 2}} \quad </math>
-<b>4)</b> <math> \;\; \displaystyle {1 \over 8} \; = \; {1 \cdot {\color{Red} 5} \over 8 \cdot {\color{Red} 5}} \; = \; {5 \over 40} \; = \; {5 \cdot {\color{Red} 5} \over 40 \cdot {\color{Red} 5}} \; = \; {25 \over 200} \; = </math>
+<math> \quad </math> Eller använd miniräknare<span style="color:black">:</span>
+<math> \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \quad\; 3,5 \quad\; = \; \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \quad </math>
+</div>
+<big>
+<b><span style="color:#931136">Omvandling av blandad form till bråk</span></b>
+</big>
+<div class="ovnE">
+Skriv den blandade formen till bråk<span>:</span>
+<math> \quad \displaystyle \boxed{\color {Limegreen} 3\,\frac{1}{\color {Red} 2}} \;\; = \;\; \frac{\color {Limegreen} 3 \, \cdot \color {Red} 2 \quad + \quad 1}{\color {Red} 2} \;\; = \;\; \frac{7}{\color {Red} 2} </math>
+<math> \quad </math> Därför att<span style="color:black">:</span>
+<math> \quad \displaystyle \color {Limegreen} 3\,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \; + \; \frac{1}{\color {Red} 2} = \frac{\color {Limegreen} 3}{1} + \frac{1}{\color {Red} 2} \; = </math>
+<math> \qquad\;\;\, \displaystyle \; = \; \frac{\color {Limegreen} 3 \cdot \color {Red} 2}{1 \cdot \color {Red} 2} \; + \; \frac{1}{\color {Red} 2} \; = \; \frac{6}{\color{Red} 2} \; + \; \frac{1}{\color{Red} 2} \; = \; \frac{7}{\color{Red} 2} </math>
+</div>
+<big>
+<b><span style="color:#931136">Regeln</span></b>
+<div class="border-divblue">
+<math> \quad \displaystyle \color {Limegreen} a\;\frac{b}{\color {Red} c} \quad = \quad \frac{\color {Limegreen} a \, \cdot \color {Red} c \quad + \quad b}{\color {Red} c} \quad </math>
+</div>
+</big>
+<big>
+<b><span style="color:#931136">Förklaring för <math> \; + \; </math> i de två rutorna ovan</span></b>
+<div class="ovnA">
+I blandade former står mellan heltalet och
+bråket ett <b><span style="color:red">osynligt</span></b> <big><big><span style="color:red">+</span></big></big>&nbsp;&nbsp;&nbsp; <math> \quad \displaystyle \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 </math> <big><big><span style="color:red">+</span></big></big> <math> \displaystyle \frac{1}{\color {Red} 2} \quad </math>
+Läs därför: &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; "Tre <b><span style="color:red">och</span></b> en halv"
+</div>
+</big>
+= <b><span style="color:#931136">Förkortning av bråk</span></b> =
+<br><div class="ovnC">
+<big>Förkorta bråken så långt som möjligt:</big>
+<b>1)</b> <math> \quad \displaystyle \frac{2}{4} \; = \; \frac{1 \cdot 2}{2 \cdot 2} \; = \; \frac{1 \cdot \cancel{\color{Red} 2}}{2 \cdot \cancel{\color{Red} 2}}  \; = \; \frac{1}{2} </math>
+<b>2)</b> <math> \quad \displaystyle \frac{6}{9} \; = \; \frac{2 \cdot 3}{3 \cdot 3} \; = \; \frac{2 \cdot \cancel{\color{Red} 3}}{3 \cdot \cancel{\color{Red} 3}}  \; = \; \frac{2}{3} </math>
+<b>3)</b> <math> \quad \displaystyle \frac{10}{15} \; = \; \frac{2 \cdot 5}{3 \cdot 5} \; = \; \; \frac{2 \cdot \cancel{\color{Red} 5}}{3 \cdot \cancel{\color{Red} 5}} \; = \; \frac{2}{3} </math>
-<math> \qquad\;\;\; \displaystyle = \; {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \; = \; {125 \over 1\,000} </math>
+<b>4)</b> <math> \quad \displaystyle \frac{8}{24} \; = \; \frac{\cancel{\color{Red} 2} \cdot 4}{\cancel{\color{Red} 2} \cdot 12} \, = \, \frac{\cancel{\color{Red} 2} \cdot 2}{\cancel{\color{Red} 2} \cdot 6} \, = \, \frac{\cancel{\color{Red} 2} \cdot 1}{\cancel{\color{Red} 2} \cdot 3} \, = \, \frac{1}{3} </math>
 <b>Metoden:</b>
-<b><span style="color:red">Multiplicera</span></b> täljaren och nämnaren med samma tal.
+Hitta en gemensam [[1.1_Om_tal#Summa_.5C.28-.5C.29_Differens_.5C.28-.5C.29_Produkt_.5C.28-.5C.29_Kvot|<b><span style="color:blue">faktor</span></b>]] hos täljaren och nämna-
+ren. <b><span style="color:red">Dividera</span></b> både täljaren och nämnaren med
+samma gemensamma faktor.
 </div>
-== <b><span style="color:#931136">Varför förlängning?</span></b> ==
+<big>
+<b><span style="color:#931136">Rekommendation</span></b>
+<div class="border-divblue">
+Förkorta alltid ett bråk när det är möjligt för att få
+mindre tal och därmed minska risken för felräknning.
+</div>
+</big>
+= <b><span style="color:#931136">Förlängning av bråk</span></b> =
 <br>
 <div class="ovnA">
-Exemplen <b>1)</b> och <b>2)</b> visar att bråken genom förläng-
+<big>Förläng bråken:</big>
-ning kan få samma nämnare, vilket gör att man t.ex.
+<b>1)</b> <math> \quad \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 3}}{4 \cdot {\color{Red} 3}}  \; = \; \frac{9}{12} </math>
-kan jämföra dem med varandra<span style="color:black">:</span> <math> \quad\;\; \displaystyle \frac{9}{12} \, > \, \frac{8}{12} </math>
+<b>2)</b> <math> \quad \displaystyle \frac{2}{3} \; = \; \frac{2 \cdot {\color{Red} 4}}{3 \cdot {\color{Red} 4}}  \; = \; \frac{8}{12} </math>
-och därmed avgöra<span style="color:black">:</span> <math> \qquad\qquad\qquad\; \displaystyle \frac{3}{4} \, > \, \frac{2}{3} </math>
+<b>3)</b> <math> \quad \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 5}}{4 \cdot {\color{Red} 5}} \; = \; \frac{15}{20} \; = \; \frac{15 \cdot {\color{Red} 5}}{20 \cdot {\color{Red} 5}} \; = \; \frac{75}{100} </math>
-Dessutom kam man addera och subtrahera dem.
+<b>4)</b> <math> \quad \displaystyle {1 \over 8} \; = \; {1 \cdot {\color{Red} 5} \over 8 \cdot {\color{Red} 5}} \; = \; {5 \over 40} \; = \; {5 \cdot {\color{Red} 5} \over 40 \cdot {\color{Red} 5}} \; = \; {25 \over 200} \; = </math>
-Exemplen <b>3)</b> och <b>4)</b> visar att bråken genom förläng-
+<math> \qquad\quad\; \displaystyle = \; {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \; = \; {125 \over 1\,000} </math>
-ning kan få en <math> \, 10</math>-potens i nämnaren, vilket t.ex.
+<b>Metoden:</b>
-gör att man direkt kan skriva dem till decimaltal.
+<b><span style="color:red">Multiplicera</span></b> täljaren och nämnaren med samma tal.
 </div>
 <big>
-<b><span style="color:#931136">Slutsats:</span></b>
+<b><span style="color:#931136">Slutsats</span></b>
 <div class="border-divblue">
 Både förkortning och förlängning bibehåller
@@ Rad 103: / Rad 188: @@
-== <b><span style="color:#931136">Addition och subtraktion av bråk</span></b> ==
+= <b><span style="color:#931136">När ska man förlänga bråk?</span></b> =
+<div class="ovnA">
+<b>1) &nbsp;&nbsp; Jämförelse av bråk:</b>
+Ex.: Vilket av bråken är större<span style="color:black">:</span> <math> \quad \displaystyle \frac{3}{4} \quad </math> eller <math> \quad \displaystyle \frac{2}{3} \quad </math> ?
+Det kan man bara avgöra genom att förlänga dem till sam-
+ma nämnare, se [[1.5_Br%C3%A5kr%C3%A4kning#F.C3.B6rl.C3.A4ngning_av_br.C3.A5k|<b><span style="color:#931136">Förlängnng av bråk</span></b>]], ex. 1 och 2<span style="color:black">:</span>
+<math> \qquad\;\; \displaystyle \frac{9}{12} \, > \, \frac{8}{12} \qquad \implies \qquad\displaystyle \frac{3}{4} \, > \, \frac{2}{3} </math>
+<b>2) &nbsp;&nbsp; Addition av bråk med olika nämnare:</b>
+Se nedan: &nbsp; <b><span style="color:#931136">Fall 2 Bråk med olika nämnare</span></b>.
+</div>
+= <b><span style="color:#931136">Addition och subtraktion av bråk</span></b> =
 <br>
-<big><big><b><span style="color:#931136">Fall 1 &nbsp; Lika nämnare</span></b></big></big>
+<big><big><b><span style="color:#931136">Fall 1 &nbsp; Bråk med samma nämnare</span></b></big></big>
 <div class="ovnE">
 <math> \quad \displaystyle \frac{1}{\color{Red} 5} \; + \; \frac{3}{\color{Red} 5} \; = \; \frac{4}{\color{Red} 5} </math>
 <math> \quad \displaystyle \frac{11}{\color{Red} {12}} \; - \; \frac{5}{\color{Red} {12}} \; = \; \frac{6}{\color{Red} {12}} \; = \; \frac{1 \cdot \cancel{6}}{2 \cdot \cancel{6}} \; = \; \frac{1}{2} </math>
-<math> \quad </math> Förkorta alltid svaret så långt som möjligt.
 <math> \quad \displaystyle \frac{5}{\color{Red} {11}} + \frac{13}{\color{Red} {11}} - \frac{9}{\color{Red} {11}} = \frac{5+13-9}{\color{Red} {11}} = \frac{9}{\color{Red} {11}} \quad </math>
@@ Rad 118: / Rad 219: @@
 <big>
-<b><span style="color:#931136">Regeln för add./subtr. av bråk med <span style="color:red">lika</span> nämnare:</span></b>
+<b><span style="color:#931136">Regeln för add./subtr. av bråk med <span style="color:red">samma</span> nämnare</span></b>
 <div class="border-divblue">
@@ Rad 128: / Rad 229: @@
-<big><big><b><span style="color:#931136">Fall 2 &nbsp; Olika nämnare</span></b></big></big>
+<big><big><b><span style="color:#931136">Fall 2 &nbsp; Bråk med olika nämnare</span></b></big></big>
-<div class="ovnE">
+<div class="ovnC">
 <math> \quad \displaystyle \frac{1}{2} \; + \; \frac{1}{3} \; = \; \frac{1 \cdot {\color{Limegreen} 3}}{2 \cdot {\color{Limegreen} 3}} \; + \; \frac{1 \cdot {\color{Limegreen} 2}}{3 \cdot {\color{Limegreen} 2}} \; = \; </math>
@@ Rad 145: / Rad 246: @@
 <big>
-<b><span style="color:#931136">Regeln för add./subtr. av bråk med <span style="color:red">olika</span> nämnare:</span></b>
+<b><span style="color:#931136">Produktmetoden för add./subtr. av bråk med <span style="color:red">olika</span> nämnare</span></b>
 <div class="border-divblue">
-Förläng bråken så att de får en <b><span style="color:red">gemen-</span></b>
+<b>1)&nbsp;</b>Förläng bråken så att de får en <b><span style="color:red">gemen-</span></b>
-<b><span style="color:red">sam nämnare</span></b> (oftast nämnarnas produkt).
+&nbsp;&nbsp;&nbsp;&nbsp;<b><span style="color:red">sam nämnare</span></b> ( = nämnarnas <b><span style="color:#931136">produkt</span></b>).
-Använd <b><span style="color:#931136">regeln för add./subtr. av bråk</span></b>
+<b>2)&nbsp;</b>Ta över den gemensamma nämnaren.
-<b><span style="color:#931136">med <span style="color:red">lika</span> nämnare</span></b>.
+&nbsp;&nbsp;&nbsp;&nbsp;Addera/subtrahera täljarna.
 </div>
 </big>
-== <b><span style="color:#931136">Multiplikation av bråk</span></b> ==
+= <b><span style="color:#931136"><small>En  bättre metod:</small><br><br>Minsta gemensamma nämnare (MGN)</span></b> =
+<div class="ovnE">
+<b><span style="color:#931136">Produktmetoden:</span></b>
+<math> \quad \displaystyle \frac{1}{6} \; + \; \frac{2}{9} \; = \; \frac{1 \cdot {\color{Limegreen} 9}}{6 \cdot {\color{Limegreen} 9}} \; + \; \frac{2 \cdot {\color{Limegreen} 6}}{9 \cdot {\color{Limegreen} 6}} \; = \; </math>
+<math> \quad \displaystyle \, = \, \frac{9}{\color{Red} {54}} \, + \, \frac{12}{\color{Red} {54}} \, = \, \frac{21}{\color{Red} {54}} \, = \, \frac{7 \cdot \cancel{\color{Red} 3}}{18 \cdot \cancel{\color{Red} 3}}  \, = \, \frac{7}{18} </math>
+<b><span style="color:#931136">Produktmetoden</span></b> hittar <b><span style="color:red">en</span></b> gemensam nämnare: <b><span style="color:red">54</span></b>.
+</div>
+<div class="ovnC">
+<b><span style="color:#931136">MGN-metoden:</span></b>
+<math> \quad \displaystyle \frac{1}{6} \; + \; \frac{2}{9} \; = \; \frac{1}{2 \cdot {\color{Red} 3}} \; + \; \frac{2}{3 \cdot {\color{Red} 3}} \; = \; </math>
+<math> \quad \displaystyle \, = \, \frac{1 \cdot {\color{Limegreen} 3}}{6 \cdot {\color{Limegreen} 3}} \; + \; \frac{2 \cdot {\color{Limegreen} 2}}{9 \cdot {\color{Limegreen} 2}} \, = \, \frac{3}{\color{Red} {18}} \, + \, \frac{4}{18}  \, = \, \frac{7}{18} </math>
+<b><span style="color:#931136">MGN-metoden</span></b> hittar <b><span style="color:red">den minsta</span></b> gem. nämnaren: <b><span style="color:red">18</span></b>.
+</div>
+<big>
+<b><span style="color:#931136">Generellt</span></b>
+<div class="border-divblue">
+<b><span style="color:#931136">MGN</span></b> = Produkt / Största gemensamma delare.
+Ex.: 54 / 3 = <b><span style="color:#931136">18</span></b>.
+</div>
+</big>
+= <b><span style="color:#931136">Multiplikation av bråk</span></b> =
 <br>
 <div class="ovnC">
@@ Rad 166: / Rad 300: @@
 <math> \quad \displaystyle \frac{3}{4} \; \cdot \; \frac{2}{3} \; = \; \frac{3 \cdot 2}{4 \cdot 3} \; = \; \frac{6}{12} \; = \; \frac{1 \cdot \cancel{6}}{2 \cdot \cancel{6}} \; = \; \frac{1}{2} </math>
-<math> \quad </math> Förkorta alltid svaret så långt som möjligt.
 </div>
 <big>
-<b><span style="color:#931136">Regeln för multiplikation av bråk:</span></b>
+<b><span style="color:#931136">Regeln för multiplikation av bråk</span></b>
 <div class="border-divblue">
 <table>
@@ Rad 186: / Rad 318: @@
-== <b><span style="color:#931136">Division av bråk</span></b> ==
+<big>
+<b><span style="color:#931136">Allmän regel för redovisning av bråkuppgifter</span></b>
+<div class="border-divblue">
+Förkorta dina svar så långt som möjligt.
+</div>
+</big>
+= <b><span style="color:#931136">Division av bråk</span></b> =
 <br>
 <div class="ovnA">
@@ Rad 192: / Rad 332: @@
 <math> \qquad\qquad\; \displaystyle \; = \; \frac{\cancel{2} \cdot 2}{\cancel{2} \cdot 3} \; = \; \frac{2}{3} </math>
-<math> \quad </math> Förkorta alltid svaret så långt som möjligt.
-----
 <math> \quad \displaystyle \frac{2}{3} \; \Big/ \; \frac{5}{7} \; = \; \frac{2}{3} \; {\color{Red} {\cdot \; \frac{7}{5}}} \; = \; \frac{2 \cdot 7}{3 \cdot 5} \; = \; \frac{14}{15} </math>
@@ Rad 204: / Rad 340: @@
 <big>
-<b><span style="color:#931136">Regeln för division av bråk:</span></b>
+<b><span style="color:#931136">Regeln för division av bråk</span></b>
 <div class="border-divblue">
 Ersätt <math> / </math> med <math> {\color{Red} {\cdot}} </math> och <b><span style="color:red">invertera</span></b> det bråk som
@@ Rad 229: / Rad 365: @@
 <big>
-<b><span style="color:#931136">Regeln för dubbelbråk:</span></b>
+<b><span style="color:#931136">Regeln för dubbelbråk</span></b>
 <div class="border-divblue">
 Ta de "yttersta" (<math> \, {\color{Red} 2} \, </math> och <math> \, {\color{Red} 9} \, </math>) till täljaren.
@@ Rad 238: / Rad 374: @@
-== <b><span style="color:#931136">Heltal som bråk</span></b> ==
+= <b><span style="color:#931136">Bråk gånger heltal</span></b> =
-<br>
-<div class="ovnE">
-<big><math> \qquad \displaystyle  9 \; = \; \frac{9}{1} \qquad </math></big>
-</div>
-<big>
-<b><span style="color:#931136">Generellt:</span></b>
-<div class="border-divblue">
-Alla heltal kan skrivas i bråkform
-genom att ge dem nämnaren <big><math> \, {\color{Red} 1} \, </math></big>.
-</div>
-</big>
-== <b><span style="color:#931136">Bråk gånger heltal</span></b> ==
 <br>
 <div class="ovnE">
@@ Rad 271: / Rad 390: @@
 <big>
-<b><span style="color:#931136">Regel:</span></b>
+<b><span style="color:#931136">Regel</span></b>
 <div class="border-divblue">
 Ta täljaren <math> \times </math> heltalet, bibehåll nämnaren.
@@ Rad 278: / Rad 397: @@
-== <b><span style="color:#931136">Bråkdel av ett tal</span></b> ==
+= <b><span style="color:#931136">Bråkdel av ett tal</span></b> =
 <br>
 <div class="ovnE">
@@ Rad 288: / Rad 407: @@
 <big>
-<b><span style="color:#931136">Regel:</span></b>
+<b><span style="color:#931136">Regel</span></b>
 <div class="border-divblue">
 Översätt <b><span style="color:red">av</span></b> till <b><span style="color:red">gånger</span></b>.
@@ Rad 301: / Rad 420: @@
 </div>
-== <b><span style="color:#931136">Tal i blandad form</span></b> ==
-<br>
-<div class="ovnC">
-<big>Skriv bråket till <u>blandad form</u>:</big>
-<math> \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \; \color {Limegreen} 3 \,, {\rm rest} \; 1 \; = \; \boxed{\color {Limegreen} 3 \,\frac{1}{\color {Red} 2}} \quad </math>
-<math> \quad </math> Eller använd miniräknare<span style="color:black">:</span>
-<math> \quad \displaystyle \frac{7}{\color {Red} 2} \; = \; 7 \, / \, \color {Red} 2 \; = \quad\; 3,5 \quad\; = \; \color {Limegreen} 3 \,\frac{1}{\color {Red} 2} \quad </math>
-</div>
-<div class="ovnC">
-<big>Skriv blandade formen till bråk:</big>
-<math> \quad \displaystyle \boxed{\color {Limegreen} 3\,\frac{1}{\color {Red} 2}} \;\; = \;\; \frac{\color {Limegreen} 3 \, \cdot \color {Red} 2 \quad + \quad 1}{\color {Red} 2} \;\; = \;\; \frac{7}{\color {Red} 2} </math>
-<math> \quad </math> Därför att<span style="color:black">:</span>
-<math> \quad \displaystyle \color {Limegreen} 3\,\frac{1}{\color {Red} 2} \; = \; \color {Limegreen} 3 \; + \; \frac{1}{\color {Red} 2} = \frac{\color {Limegreen} 3}{1} + \frac{1}{\color {Red} 2} \; = </math>
-<math> \qquad\;\;\, \displaystyle \; = \; \frac{\color {Limegreen} 3 \cdot \color {Red} 2}{1 \cdot \color {Red} 2} \; + \; \frac{1}{\color {Red} 2} \; = \; \frac{6}{\color{Red} 2} \; + \; \frac{1}{\color{Red} 2} \; = \; \frac{7}{\color{Red} 2} </math>
-</div>
-<big>
-<b><span style="color:#931136">Slutsats:</span></b>
-<div class="border-divblue">
-I blandade former står mellan heltalet
-och bråket ett osynligt &nbsp; <big><big><span style="color:red">+</span></big></big> &nbsp; .
-</div>
-</big>
-<big>
-<b><span style="color:#931136">Regeln för att skriva en blandad form till bråk:</span></b>
-<div class="border-divblue">
-<math> \quad \displaystyle \color {Limegreen} a\;\frac{b}{\color {Red} c} \quad = \quad \frac{\color {Limegreen} a \, \cdot \color {Red} c \quad + \quad b}{\color {Red} c} \quad </math>
-</div>
-</big>
@@ Rad 351: / Rad 426: @@
-[[Matte:Copyrights|Copyright]] © 2010-2017 Math Online Sweden AB. All Rights Reserved.
+[[Matte:Copyrights|Copyright]] © 2023 <b><span style="color:blue">TechPages AB</span></b>. All Rights Reserved.

Skillnad mellan versioner av "1.5 Tal i bråkform"

Nuvarande version från 11 januari 2023 kl. 19.53

Heltal som bråk

Blandad form

Förkortning av bråk

Förlängning av bråk

När ska man förlänga bråk?

Addition och subtraktion av bråk

En bättre metod:Minsta gemensamma nämnare (MGN)

Multiplikation av bråk

Division av bråk

Dubbelbråk

Bråk gånger heltal

Bråkdel av ett tal

Navigeringsmeny

Sök

En bättre metod:

Minsta gemensamma nämnare (MGN)