Skillnad mellan versioner av "4.2 Funktionsbegreppet"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (20 mellanliggande versioner av samma användare visas inte) | |||
| Rad 3: | Rad 3: | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
{{Not selected tab|[[4.1 Koordinatsystem, värdetabeller och grafer| << Förra avsnitt]]}} | {{Not selected tab|[[4.1 Koordinatsystem, värdetabeller och grafer| << Förra avsnitt]]}} | ||
| − | {{Selected tab|[[4.2 | + | {{Selected tab|[[4.2 Funktionsbegreppet|Genomgång]]}} |
| − | {{Not selected tab|[[4.2 Övningar till Funktioner|Övningar]]}} | + | {{Not selected tab|[[Media: 4_2_Graf-tabell-formel_Onv.pdf|Övningar]]}} |
| + | {{Not selected tab|[[Media: 4_2_Graf-tabell-formel_Facit.pdf|Facit]]}} | ||
| + | <!-- {{Not selected tab|[[4.2 Övningar till Funktioner|Övningar]]}} --> | ||
{{Not selected tab|[[4.3 En funktions definitions- och värdemängd|Nästa avsnitt >> ]]}} | {{Not selected tab|[[4.3 En funktions definitions- och värdemängd|Nästa avsnitt >> ]]}} | ||
| + | <!-- {{Not selected tab|[[Olika matematiska modeller|Nästa avsnitt >> ]]}} --> | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| Rad 43: | Rad 46: | ||
</td> | </td> | ||
<td> [[Image: Kontinuerlig_prisfunktion_ris.jpg]]</td> | <td> [[Image: Kontinuerlig_prisfunktion_ris.jpg]]</td> | ||
| − | <td> | + | <td> |
| − | | + | |
| − | | + | |
| − | | + | |
| Rad 59: | Rad 62: | ||
<math> \quad\; y \, </math> är priset i kr. <math> \quad\;\;\; \color{Red} x \, </math> är mängden i liter. | <math> \quad\; y \, </math> är priset i kr. <math> \quad\;\;\; \color{Red} x \, </math> är mängden i liter. | ||
| − | Grafen till funktionen <math> \, y = 30\,x </math> visar priset <math> y \, </math> som en funktion av <math> x </math>. | + | Grafen till funktionen <math> \, y = 30\,x </math> visar priset <math> y \, </math> som en funktion av <math> x </math>. Grafen är en <b><span style="color:red">rät linje</span></b> vars lutning är <math> \, 30 </math>. |
| − | + | ||
| − | Grafen | + | |
<math> y = 30\, x </math> är en <b><span style="color:red">funktion</span></b> som är definierad endast för alla reella tal <math> \color{Red}{x \geq 0} \, </math>, därför att det inte finns några negativa mängder. | <math> y = 30\, x </math> är en <b><span style="color:red">funktion</span></b> som är definierad endast för alla reella tal <math> \color{Red}{x \geq 0} \, </math>, därför att det inte finns några negativa mängder. | ||
| Rad 87: | Rad 88: | ||
<math> \qquad\qquad\qquad\qquad\qquad\;\; </math> <div class="smallBoxVariant"><span style="color:red">beroende var.</span> = f (<span style="color:red">oberoende var.</span>)</div> | <math> \qquad\qquad\qquad\qquad\qquad\;\; </math> <div class="smallBoxVariant"><span style="color:red">beroende var.</span> = f (<span style="color:red">oberoende var.</span>)</div> | ||
| − | </span></b></big> | + | </span> |
| + | <math> \qquad\qquad\qquad\qquad\qquad\qquad y\, = \, f(x) \quad </math> Läs<span>:</span> <math> \; y\, = \, f \; {\text av} \; x </math> | ||
| + | </b></big> | ||
</div> | </div> | ||
| Rad 104: | Rad 107: | ||
| − | [[Matte:Copyrights|Copyright]] © | + | [[Matte:Copyrights|Copyright]] © 2022 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved. |
Nuvarande version från 26 februari 2022 kl. 16.13
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
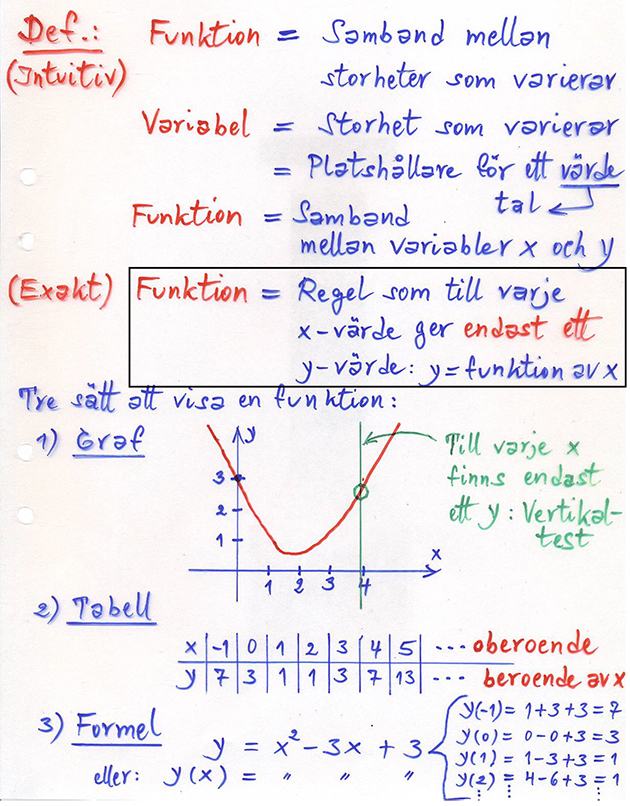
Vad är en funktion?
Exempel Funktion
|
En torghandlare säljer färskpressad granatäppeljuice för \( \, 30 \) kr per liter. \( {\color{Red} 1} \; \) liter ljuice kostar \( {\color{Red} 1} \cdot 30 \;{\rm kr,} \) \( {\color{Red} 2} \; \) liter ljuice kostar \( {\color{Red} 2} \cdot 30 \;{\rm kr,} \) \( {\color{Red} 3} \; \) liter ljuice kostar \( {\color{Red} 3} \cdot 30 \;{\rm kr,} \qquad \cdots \) \( {\color{Red} x} \; \) liter ljuice kostar \( {\color{Red} x} \cdot 30 \;{\rm kr} \) eller \( 30\;{\color{Red} x} \;{\rm kr.} \) Därför är prisfunktionen: \( y = 30\;{\color{Red} x} \, , \quad
{\rm där } \quad {\color{Red} x}\,= {\rm {\color{Red} {reellt\;tal}}\,.} \)
|
 |
|
\( \quad\; y \, \) är priset i kr. \( \quad\;\;\; \color{Red} x \, \) är mängden i liter.
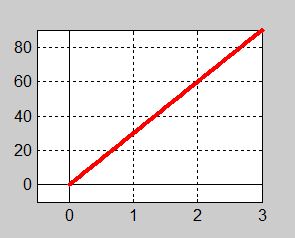
Grafen till funktionen \( \, y = 30\,x \) visar priset \( y \, \) som en funktion av \( x \). Grafen är en rät linje vars lutning är \( \, 30 \).
\( y = 30\, x \) är en funktion som är definierad endast för alla reella tal \( \color{Red}{x \geq 0} \, \), därför att det inte finns några negativa mängder.
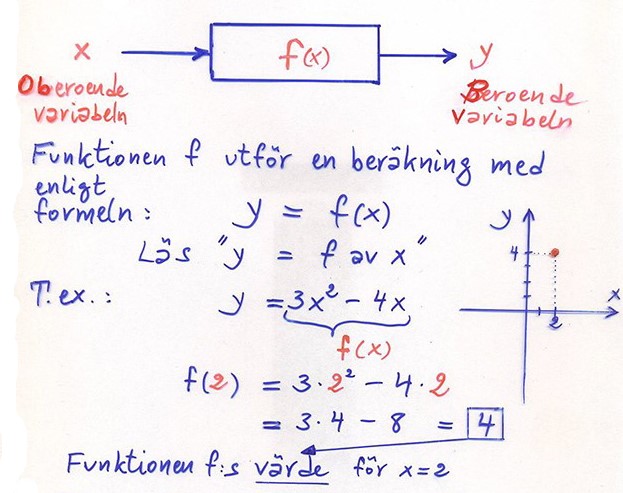
Symbolen f(x)
Funktionen y = f(x) som en "svart låda":
\( \; \color{Red} x \;\; \) kallas för den oberoende variabeln eftersom den kan anta ett värde oberoende av \( \; y \; \).
\( \; \color{Red} y \;\; \) kallas för den beroende variabeln eftersom dess värde alltid är beroende av \( \; x \; \).
Det är variabelns plats som avgör vilken som är beroende och vilken som är oberoende:
\( \qquad\qquad\qquad\qquad\qquad\;\; \)\( \qquad\qquad\qquad\qquad\qquad\qquad y\, = \, f(x) \quad \) Läs: \( \; y\, = \, f \; {\text av} \; x \)
Copyright © 2022 TechPages AB. All Rights Reserved.
