Skillnad mellan versioner av "5.6 Implikation och ekvivalens"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (En mellanliggande version av samma användare visas inte) | |||
| Rad 5: | Rad 5: | ||
{{Selected tab|[[5.6 Implikation och ekvivalens|Genomgång]]}} | {{Selected tab|[[5.6 Implikation och ekvivalens|Genomgång]]}} | ||
{{Not selected tab|[[5.6 Övningar till Implikation och ekvivalens|Övningar]]}} | {{Not selected tab|[[5.6 Övningar till Implikation och ekvivalens|Övningar]]}} | ||
| + | {{Not selected tab|[[5.7 Problemlösning: Cirkel-kvadrat problemet|Nästa avsnitt >>]]}} | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| Rad 59: | Rad 60: | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
<big><b> | <big><b> | ||
| − | Är [[5.3_Pythagoras_sats#Ett_bevis_av_Pythagoras_sats|<span style="color:#931136">Pythagoras sats (påståendet)</span>]] en implikation eller en ekvivalens? | + | Är [[5.3_Pythagoras_sats#Ett_bevis_av_Pythagoras_sats|<span style="color:#931136">Pythagoras sats (påståendet i 5.3)</span>]] en implikation eller en ekvivalens? |
Och i så fall mellan vilka utsagor? | Och i så fall mellan vilka utsagor? | ||
| − | Är [[5.3_Pythagoras_sats#Ett_bevis_av_Pythagoras_sats|<span style="color:#931136">beviset av Pythagoras sats</span>]] ett bevis för implikation eller för ekvivalens? | + | Är [[5.3_Pythagoras_sats#Ett_bevis_av_Pythagoras_sats|<span style="color:#931136">beviset av Pythagoras sats (5.3)</span>]] ett bevis för implikation eller för ekvivalens? |
</b></big> | </b></big> | ||
</div> | </div> | ||
Nuvarande version från 25 mars 2020 kl. 13.28
| <<< Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
Implikation och ekvivalens är:
- Logiska verktyg i matematisk bevisföring, se förra avsnitt.
- Logiska operatorer som kan skrivas mellan två utsagor.
En utsaga är ett påstående eller en sats som antingen är sant eller falskt.
Implikation symboliseras med \( \;\; \implies \;\; \), ekvivalens med \( \;\; \iff \;\; \).
- Kan användas även i alla vardagliga sammanhang, se exemplen:
Exempel på implikation
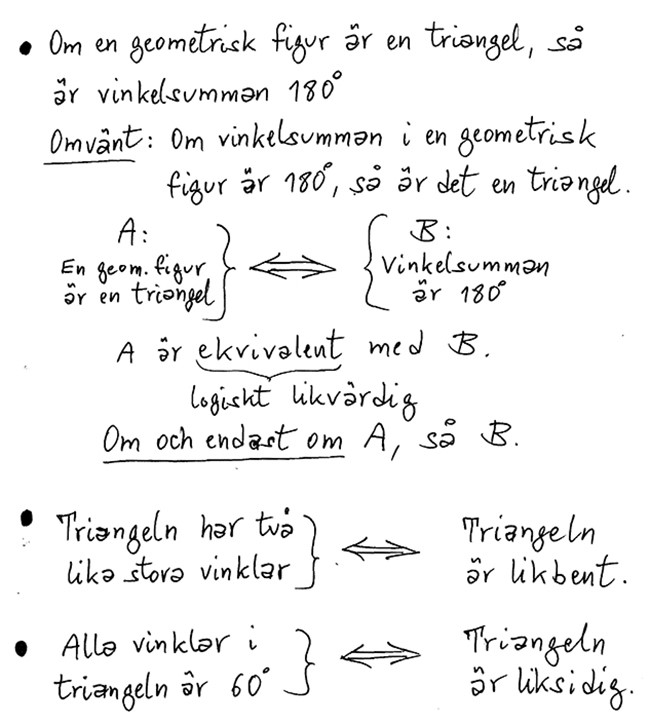
En implikation som gäller i båda riktningar kallas för ekvivalens.
En ekvivalens är en implikation och dess omvända.
Ekvivalens betyder (logisk) likvärdighet. På latin: ekvi = lik, valens = värdighet.
\( \; \iff \;\; \) sätts mellan utsagor och ersätter \( \; = \; \) som sätts mellan uttryck eller tal.
Exempel på ekvivalens
Dagens testfråga
Är Pythagoras sats (påståendet i 5.3) en implikation eller en ekvivalens?
Och i så fall mellan vilka utsagor?
Är beviset av Pythagoras sats (5.3) ett bevis för implikation eller för ekvivalens?
Copyright © 2020 TechPages AB. All Rights Reserved.