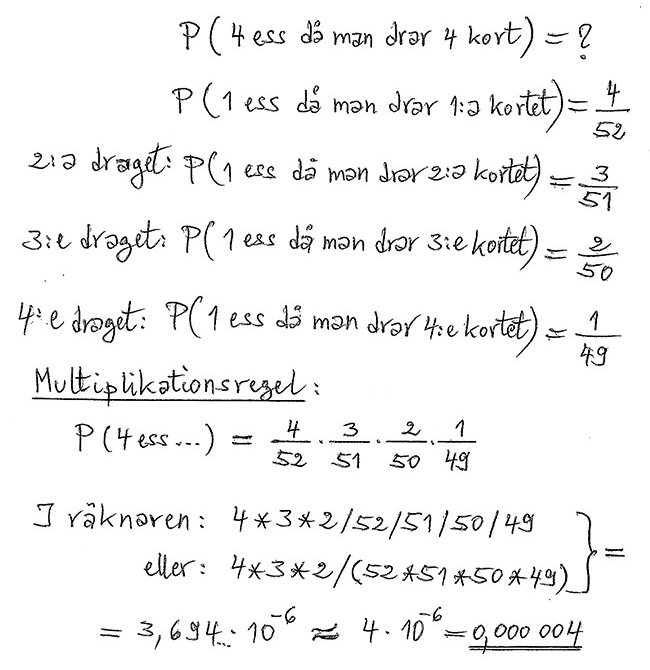Skillnad mellan versioner av "6.2 Beräkning av sannolikheter"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (5 mellanliggande versioner av samma användare visas inte) | |||
| Rad 39: | Rad 39: | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
<big> | <big> | ||
| − | Är <math> \, A \, </math> och <math> \, B \, </math> två händelser som inträffar efter varandra och är | + | Är <math> \, A \, </math> och <math> \, B \, </math> två oberoende händelser som inträffar efter varandra och är |
<math> \; P(A) \, </math> sannolikheten för händelsen <math> \, A \, </math> och <math> \, P(B) \, </math> sannolikheten för händelsen <math> \, B \, </math> | <math> \; P(A) \, </math> sannolikheten för händelsen <math> \, A \, </math> och <math> \, P(B) \, </math> sannolikheten för händelsen <math> \, B \, </math> | ||
| Rad 49: | Rad 49: | ||
</div> | </div> | ||
| − | + | <!-- | |
= <b><span style="color:#931136">Dagens inlämningsuppgift</span></b> = | = <b><span style="color:#931136">Dagens inlämningsuppgift</span></b> = | ||
<div class="ovnA"><big> | <div class="ovnA"><big> | ||
| − | :Lös uppgifterna | + | :Lös uppgifterna 7201-7204 i 1b-boken, sid 241 (1c-boken sid 225, 6201-6204). |
:Skriv ren dina lösningar tydliga, läsliga och strukturerade på ett A4-blad. | :Skriv ren dina lösningar tydliga, läsliga och strukturerade på ett A4-blad. | ||
| Rad 67: | Rad 67: | ||
= <b><span style="color:#931136">Dagens övningar</span></b> = | = <b><span style="color:#931136">Dagens övningar</span></b> = | ||
<div class="ovnE"> | <div class="ovnE"> | ||
| + | |||
<big> | <big> | ||
<b><span style="color:#931136"> Gör övningarna i boken Origo 1b:</span></b> | <b><span style="color:#931136"> Gör övningarna i boken Origo 1b:</span></b> | ||
| Rad 72: | Rad 73: | ||
---- | ---- | ||
| − | Sidorna | + | Sidorna 241-242. |
---- | ---- | ||
| − | <b><span style="color:#931136"> I Origo 1c:</span></b> Sidorna | + | <b><span style="color:#931136"> I Origo 1c:</span></b> Sidorna 225-226. |
---- | ---- | ||
| Rad 83: | Rad 84: | ||
</big> | </big> | ||
</div> | </div> | ||
| − | + | --> | |
Nuvarande version från 3 maj 2022 kl. 13.52
| <<< Förra avsnitt | Innehåll Matte 1b | Genomgång | Övningar | Nästa avsnitt >> |
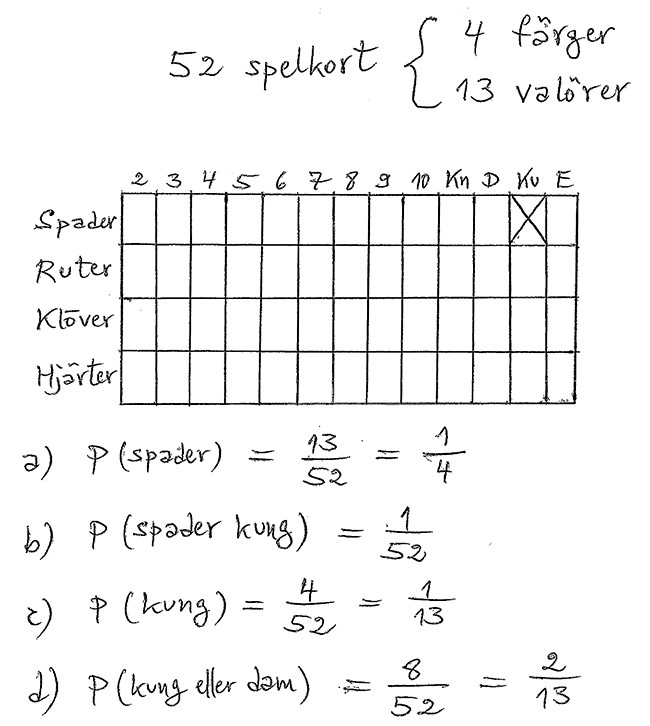
Kortlek
Flera drag ur kortleken efter varandra utan att lägga tillbaka
Beräkna sannolikheten för att få fyra ess då man drar fyra kort ur en kortlek.
Lösning:
Multiplikationsregeln
Är \( \, A \, \) och \( \, B \, \) två oberoende händelser som inträffar efter varandra och är
\( \; P(A) \, \) sannolikheten för händelsen \( \, A \, \) och \( \, P(B) \, \) sannolikheten för händelsen \( \, B \, \)
så gäller: \( \qquad\qquad\quad \)\( P(A \; \color{Red}{\text{och}} \; B) \, = \, P(A) \; \color{Red}\cdot \; P(B)\)
Exempel ovan: P(4 ess ... ).
Copyright © 2020 TechPages AB. All Rights Reserved.