Skillnad mellan versioner av "6.7 Komplementhändelse"
Från Mathonline
Taifun (Diskussion | bidrag) (Skapade sidan med '__NOTOC__ {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | style="border-bottom:1px solid #797979" width="5px" | {{Not selected tab|6.6 Beroen...') |
Taifun (Diskussion | bidrag) m |
||
| (22 mellanliggande versioner av samma användare visas inte) | |||
| Rad 5: | Rad 5: | ||
{{Not selected tab|[[Matte 1b Innehållsförteckning|Innehåll Matte 1b]]}} | {{Not selected tab|[[Matte 1b Innehållsförteckning|Innehåll Matte 1b]]}} | ||
{{Selected tab|[[6.7 Komplementhändelse|Genomgång]]}} | {{Selected tab|[[6.7 Komplementhändelse|Genomgång]]}} | ||
| − | {{Not selected tab|[[6.7 Övningar till Komplementhändelse|Övningar]]}} | + | {{Not selected tab|[[Förberedelser inför NP Matte 1b|Gammalt NP Matte 1b]]}} |
| − | {{Not selected tab|[[6.8 | + | <!-- {{Not selected tab|[[6.7 Övningar till Komplementhändelse|Övningar]]}} --> |
| + | {{Not selected tab|[[6.8 Vad handlar statistik om?|Nästa avsnitt >> ]]}} | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| − | = <b><span style="color:#931136"> | + | = <b><span style="color:#931136">Vad är en komplementhändelse?</span></b> = |
<div class="ovnE"> | <div class="ovnE"> | ||
| − | <big>Titta på detta [https://www.youtube.com/watch?v= | + | <big>Titta på detta [https://www.youtube.com/watch?v=6QnCCN2aeM4 <span style="color:#931136"><b>videoklipp</b> </span>] (8:24 min).</big> |
</div> | </div> | ||
| − | = <b><span style="color:#931136">Regler för | + | = <b><span style="color:#931136">Regler för komplementhändelse</span></b> = |
<div class="border-divblue"> | <div class="border-divblue"> | ||
<big> | <big> | ||
| − | + | Händelsen A är <b><span style="color:red">komplementhändelse</span></b> till händelsen B, | |
| − | + | om A och B tillsammans utgör alla möjliga utfall. | |
| − | + | Då gäller: <math> \qquad\; </math> <div class="smallBoxVariant"><math> P(A) \; = \; 1 \, - \, P(B)</math></div> | |
| − | + | Borde användas om P(B) är enklare att beräkna än P(A). | |
| − | + | ||
| − | + | ||
</big> | </big> | ||
</div> | </div> | ||
| Rad 34: | Rad 33: | ||
<big><big> | <big><big> | ||
| − | Ytterligare exempel på | + | Ytterligare exempel på när komplementhändelse borde användas: |
</big></big> | </big></big> | ||
| − | = <b><span style="color:#931136"> | + | = <b><span style="color:#931136">Tre olika defekt på bilar</span></b> = |
<div class="ovnC"> | <div class="ovnC"> | ||
| − | <big> | + | <big> |
| + | 5% av alla bilar i Sverige kör med defekt belysning, 10% med defekta däck och | ||
| − | + | 15% med defekta bromsar. Defekterna är oberoende av varandra. | |
| − | < | + | Hur stor är sannolikheten att en slumpvis utvald bil har <b><span style="color:red">minst en defekt</span></b>? |
| − | |||
| + | Lösning: | ||
| − | + | [[Image: Tre defekt hos bilar.jpg]] | |
| − | + | </big> | |
| − | [[Image: | + | |
</div> | </div> | ||
| − | + | <!-- | |
= <b><span style="color:#931136">Dagens inlämningsuppgift</span></b> = | = <b><span style="color:#931136">Dagens inlämningsuppgift</span></b> = | ||
<div class="ovnA"><big> | <div class="ovnA"><big> | ||
| − | :Lös uppgifterna | + | :Lös uppgifterna 7226-7228 i 1b-boken, sid 248 (1c-boken sid 232, 6226-6228). |
:Skriv ren dina lösningar tydliga, läsliga och strukturerade på ett A4-blad. | :Skriv ren dina lösningar tydliga, läsliga och strukturerade på ett A4-blad. | ||
| Rad 70: | Rad 69: | ||
= <b><span style="color:#931136">Dagens övningar</span></b> = | = <b><span style="color:#931136">Dagens övningar</span></b> = | ||
| − | |||
| − | |||
<div class="ovnE"> | <div class="ovnE"> | ||
<big> | <big> | ||
| Rad 78: | Rad 75: | ||
---- | ---- | ||
| − | | + | Sidorna 248-249. |
---- | ---- | ||
| − | <b><span style="color:#931136"> I Origo 1c:</span></b> | + | <b><span style="color:#931136"> I Origo 1c:</span></b> Sidorna 232-233. |
---- | ---- | ||
| Rad 89: | Rad 86: | ||
</big> | </big> | ||
</div> | </div> | ||
| − | + | --> | |
| − | + | ||
Nuvarande version från 4 maj 2022 kl. 14.52
| <<< Förra avsnitt | Innehåll Matte 1b | Genomgång | Gammalt NP Matte 1b | Nästa avsnitt >> |
Vad är en komplementhändelse?
Titta på detta videoklipp (8:24 min).
Regler för komplementhändelse
Händelsen A är komplementhändelse till händelsen B,
om A och B tillsammans utgör alla möjliga utfall.
Då gäller: \( \qquad\; \)\( P(A) \; = \; 1 \, - \, P(B)\)
Borde användas om P(B) är enklare att beräkna än P(A).
Ytterligare exempel på när komplementhändelse borde användas:
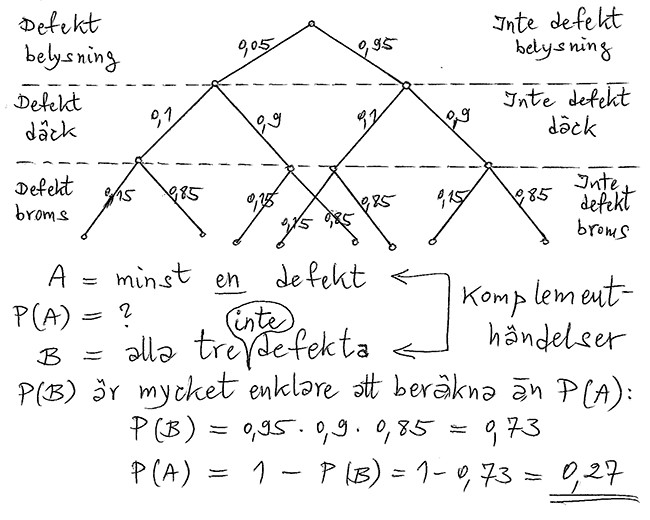
Tre olika defekt på bilar
5% av alla bilar i Sverige kör med defekt belysning, 10% med defekta däck och
15% med defekta bromsar. Defekterna är oberoende av varandra.
Hur stor är sannolikheten att en slumpvis utvald bil har minst en defekt?
Lösning:
Copyright © 2020 TechPages AB. All Rights Reserved.