Skillnad mellan versioner av "3.3 Ekvationer"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (13 mellanliggande versioner av samma användare visas inte) | |||
| Rad 13: | Rad 13: | ||
| − | + | = <b><span style="color:#931136">Varför ekvationer?</span></b> = | |
| − | + | ||
<div class="ovnE"> | <div class="ovnE"> | ||
| + | <big> | ||
<b>Exempel på en textuppgift:</b> | <b>Exempel på en textuppgift:</b> | ||
<br> | <br> | ||
| Rad 39: | Rad 39: | ||
\end{array}</math> | \end{array}</math> | ||
</div> | </div> | ||
| − | |||
<b>Svar:</b> Flaskan kostar <math> \, {\color{Red} {2 \; {\rm kr\,}}}</math>. | <b>Svar:</b> Flaskan kostar <math> \, {\color{Red} {2 \; {\rm kr\,}}}</math>. | ||
| + | För mer info om hur man ställer upp en ekvation | ||
| − | + | och om lösningsmetoder se: | |
| − | + | ||
[[3.6_Användning_av_ekvationer#Metoden_att_st.C3.A4lla_upp_en_ekvation_utifr.C3.A5n_en_textuppgift|<b><span style="color:blue">Metoden att ställa upp en ekvation utifrån en textuppgift</span></b>]], | [[3.6_Användning_av_ekvationer#Metoden_att_st.C3.A4lla_upp_en_ekvation_utifr.C3.A5n_en_textuppgift|<b><span style="color:blue">Metoden att ställa upp en ekvation utifrån en textuppgift</span></b>]], | ||
[[3.3_Ekvationer#1._.C2.A0_.C3.96vert.C3.A4ckningsmetoden|<b><span style="color:blue">Övertäckningsmetoden</span></b>]] <math> \quad </math> och <math> \quad </math> [[3.3_Ekvationer#2._.C2.A0_Allm.C3.A4n_metod|<b><span style="color:blue">Allmän metod</span></b>]]. | [[3.3_Ekvationer#1._.C2.A0_.C3.96vert.C3.A4ckningsmetoden|<b><span style="color:blue">Övertäckningsmetoden</span></b>]] <math> \quad </math> och <math> \quad </math> [[3.3_Ekvationer#2._.C2.A0_Allm.C3.A4n_metod|<b><span style="color:blue">Allmän metod</span></b>]]. | ||
| + | </big> | ||
</div> | </div> | ||
| − | + | = <b><span style="color:#931136">Vad är en ekvation?</span></b> = | |
| − | + | ||
<math> \qquad\quad </math>[[Image: Ekvation Obekant VL HL_350.jpg]] | <math> \qquad\quad </math>[[Image: Ekvation Obekant VL HL_350.jpg]] | ||
<br> | <br> | ||
| Rad 71: | Rad 70: | ||
| − | :<big><big><big><b><span style="color:#931136"> | + | :<big><big><big><b><span style="color:#931136">Vad är en lösning?</span></b></big></big></big> |
<div class="border-divblue"> | <div class="border-divblue"> | ||
| Rad 86: | Rad 85: | ||
</big> | </big> | ||
</div> | </div> | ||
| + | |||
<big><big>Om kontrollen ovan säger man: Lösningen <b><span style="color:red">satisfierar</span></b> (uppfyller) ekvationen.</big></big> | <big><big>Om kontrollen ovan säger man: Lösningen <b><span style="color:red">satisfierar</span></b> (uppfyller) ekvationen.</big></big> | ||
| Rad 273: | Rad 273: | ||
| − | [[Matte:Copyrights|Copyright]] © | + | [[Matte:Copyrights|Copyright]] © 2022 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved. |
Nuvarande version från 15 december 2022 kl. 09.54
| << Förra avsnitt | Genomgång | Quiz | Övningar | Nästa avsnitt >> |
Varför ekvationer?
Exempel på en textuppgift:
- Kalle köper en flaska dryck som kostar \( \, 18 \, \) kr med pant.
- Drycken (innehållet) kostar \( \, 14 \, \) kr mer än panten (flaskan).
- Hur mycket kostar flaskan?
Utan ekvation svarar de flesta 4 kr, vilket är fel.
Lösning med ekvation: \( \quad\;\;\; x \; = \; {\rm flaskans\;pris} \)
- \[ \qquad\qquad\;\; x \, + \, 14 \; = \; {\rm dryckens\;pris} \]
- \[\begin{array}{rcl} x \, + \, (x \, + \, 14) & = & 18 \\ x \, + \, x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 & = & 18 \\ 2\,x \, & = & 4 \\ x \, & = & {\color{Red} 2} \end{array}\]
Svar: Flaskan kostar \( \, {\color{Red} {2 \; {\rm kr\,}}}\).
För mer info om hur man ställer upp en ekvation
och om lösningsmetoder se:
Metoden att ställa upp en ekvation utifrån en textuppgift,
Övertäckningsmetoden \( \quad \) och \( \quad \) Allmän metod.
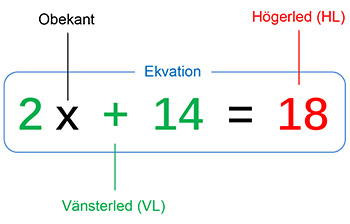
Vad är en ekvation?
En ekvation är en likhet mellan två uttryck,
har alltid formen VL = HL och innehåller
minst en variabel, kallad obekant.
Ex.: \( \qquad\quad 2\,x \; + \; 14 \; = \; 18 \)
Ekvationens lösning: \( \quad\; \)
- Vad är en lösning?
Kontroll: Sätt in lösningen i ekvationen.
VL \( \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 \)
HL \( \, = \, 18 \)
VL \( = \) HL \( \, \implies \, x = {\color{Red} 2} \) är en lösning.
Kontroll kallas ibland även för prövning.
Om kontrollen ovan säger man: Lösningen satisfierar (uppfyller) ekvationen.
Men hur får man lösningen? Det finns två lösningsmetoder:
1. Övertäckningsmetoden
Exemplet ovan:
\( 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x \)
\( \;\, {\color{Red} ?} \;\;\; + \; 14 \; = \; 18 \)
\( \;\, {\color{Red} 4} \;\;\; + \; 14 \; = \; 18 \)
\( \;\, \Downarrow \)
\( \, 2 \, \cdot \; x \;\; = \;\, {\color{Red} 4} \qquad\quad {\color{Red} {\rm Täck\;över\;}} x \)
\( \, 2 \, \cdot \; \)\( \, 2 \, \cdot \; {\color{Red} ?} \;\; = \;\; 4 \)
\( \, 2 \, \cdot \; {\color{Red} 2} \;\; = \;\; 4 \)
\( \quad\;\;\; \Downarrow \)
2. Allmän metod
Exempel:
- \[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad | & {\color{Red} {- \, 14}} \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ 2 \cdot x \, & = & 4 & \qquad | & {\color{Red} {/ \; 2}} \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x \, & = & 2 & & \end{array}\]
Skrivsättet \( \quad\;\;\, | \quad {\color{Red} {- \, 14}} \quad\;\;\, \) är en kommentar och betyder:
- Subtrahera \( \, 14 \, \) från ekvationens båda led.
Kommentaren \( \;\; | \quad {\color{Red} {/ \; 2}} \;\; \) betyder:
- Dividera ekvationens båda led med \( \, 2 \).
Den allmänna metoden steg för steg
Steg 1
Förenkla uttrycken i ekvationens båda led
så långt som möjligt. I exemplet ovan:
- \[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & & \end{array}\]
Steg 2
Utför samma operation på båda leden:
- \[\begin{array}{rcl} 2\,x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} \\ 2\,x \, & = & 4 \end{array}\]
Vilken operation?
Den inversa operation som isolerar \( x\)-termen.
\( \;\;\; {\color{Red} {- \, 14}} \, \) är den inversa operationen till \( \, + \, 14 \)
Steg 3
Utför samma operation på båda leden:
- \[\begin{array}{rclcl} \quad\; 2 \cdot x \, & = & 4 & & \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x & = & 2 & & \end{array}\]
Vilken operation?
Den inversa operation som isolerar \( \, x \, \).
\( \quad\;\; {\color{Red} {/ \; 2}} \, \) är den inversa operationen till \( \, \cdot \; 2 \)
Den allmänna metodens filosofi:
Betrakta ekvationen som en våg i balans.
HL och VL är vågens skålar. Likhetsteck-
net betyder att vågens skålar är i balans.
Bibehåll balansen genom att utföra:
\( \;\;\; \) Samma operation på båda leden !
Välj alltid den inversa operationen till den
operation som binder \( \, x \, \) till dess omgivning.
När saknar en ekvation lösning?
Exempel:
\(\begin{array}{rcl} 2\,x \, - \, 2\, (3 \, + \, x ) & = & 8 \\ 2\,x \, - \, 6 \, - \, 2\,x & = & 8 \\ - \, 6 & = & 8 \quad {\color{Red} {\rm{Motsägelse!}}} \\ & \Downarrow & \end{array}\)
\( \qquad\quad \) Ekvationen saknar lösning.
När är alla tal lösningar till en ekvation?
Exempel:
\(\begin{array}{rcl} \;\; x \, - \, (4 \, + \, x ) & = & -4 \\ x \, - \, 4 \, - \, x & = & -4 \\ - \, 4 & = & -4 \quad {\color{Red} {\rm{Alltid\;sant!}}} \\ & \Downarrow & \end{array}\)
\( \;\; \) Alla tal är lösningar till ekvationen. Eller:
\( \;\; \) Ekvationen har oändligt många lösningar.
Copyright © 2022 TechPages AB. All Rights Reserved.