Skillnad mellan versioner av "5.1 Räta linjens ekvation i k-form"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (2 mellanliggande versioner av samma användare visas inte) | |||
| Rad 5: | Rad 5: | ||
{{Not selected tab|[[Matte 1b Innehållsförteckning|Innehållsförteckning]]}} | {{Not selected tab|[[Matte 1b Innehållsförteckning|Innehållsförteckning]]}} | ||
{{Selected tab|[[5.1 Räta linjens ekvation i k-form|Genomgång]]}} | {{Selected tab|[[5.1 Räta linjens ekvation i k-form|Genomgång]]}} | ||
| − | {{Not selected tab|[[ | + | {{Not selected tab|[[Media: 5_1_Rata_lin_Ovn.pdf|Övningar]]}} |
| + | {{Not selected tab|[[Media: 5_1_Rata_lin_Facit.pdf|Facit]]}} | ||
{{Not selected tab|[[5.2 Formeln för räta linjens lutning|Nästa avsnitt >> ]]}} | {{Not selected tab|[[5.2 Formeln för räta linjens lutning|Nästa avsnitt >> ]]}} | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
| Rad 22: | Rad 23: | ||
<div class="ovnE"> | <div class="ovnE"> | ||
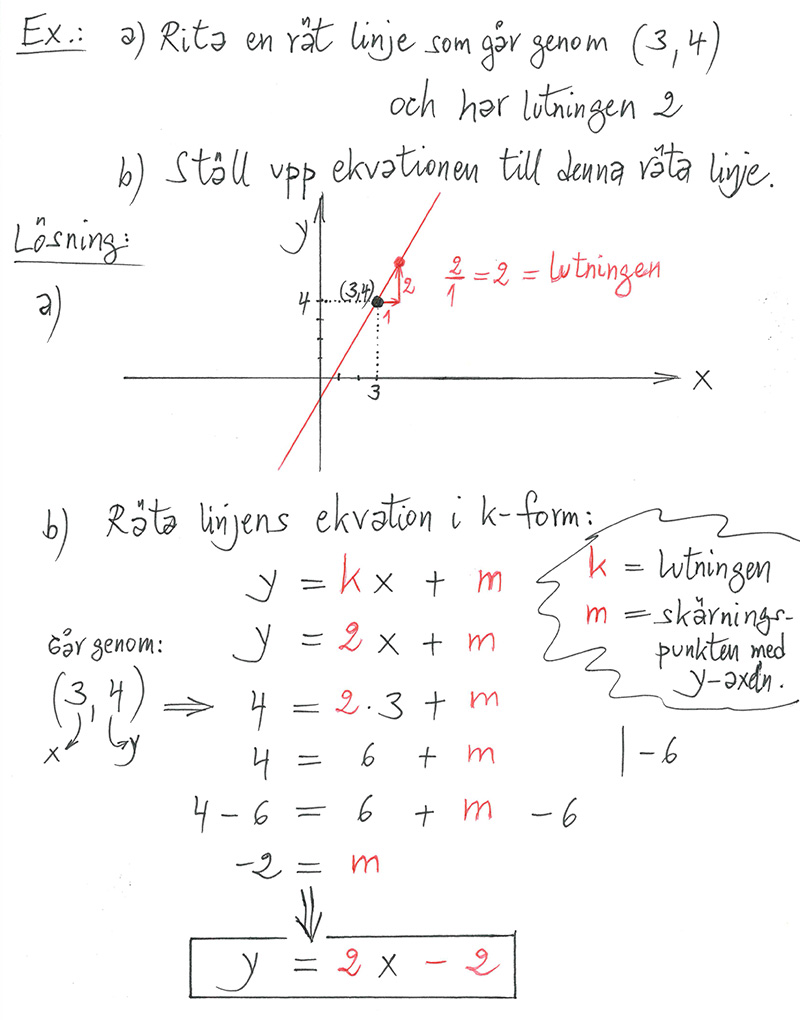
=== <b><span style="color:#931136">Räta linjens graf och ekvation</span></b> === | === <b><span style="color:#931136">Räta linjens graf och ekvation</span></b> === | ||
| − | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: | + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 5_1_Rata_linjens_ekv _k_form.jpg]] |
</div> | </div> | ||
=== <b><span style="color:#931136">Linjen har lutningen <math> k = 2 </math> och skär y-axeln i <math> m = -2 </math>.</span></b> === | === <b><span style="color:#931136">Linjen har lutningen <math> k = 2 </math> och skär y-axeln i <math> m = -2 </math>.</span></b> === | ||
Nuvarande version från 30 mars 2022 kl. 07.31
| << Förra avsnitt | Innehållsförteckning | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Räta linjen och dess funktion, här kallad "ekvation"
OBS! Begreppet "ekvation" har här en annan betydelse än i algebra.
Då betydde det likhet mellan två uttryck med EN obekant.
Här betyder det en funktion (formel), närmare bestämt en linjär funktion.
Räta linjens graf och ekvation
Linjen har lutningen \( k = 2 \) och skär y-axeln i \( m = -2 \).
Copyright © 2022 TechPages AB. All Rights Reserved.
