Skillnad mellan versioner av "1.3 Decimaltal+"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m (→Exempel 1) |
||
| Rad 38: | Rad 38: | ||
'''Lösning:''' | '''Lösning:''' | ||
| − | :Första decimalen | + | :Första decimalen <math> \, {\color{LimeGreen} 1} \, </math> har positionen <strong><span style="color:#93C800">tiondel</span></strong> och därmed värdet <math> \, {\color{LimeGreen} 1} \cdot 0,1 \, = \, {\color{Red}{0,1}} </math>. |
| − | :Andra decimalen | + | :Andra decimalen <math> \, {\color{LimeGreen} 7} \, </math> har positionen <strong><span style="color:#93C800">hundradel</span></strong> och därmed värdet <math> \, {\color{LimeGreen} 7} \cdot 0,01 \, = \, {\color{Red}{0,07}} \, </math>. |
| − | :Tredje decimalen | + | :Tredje decimalen <math> \, {\color{LimeGreen} 8} \, </math> har positionen <strong><span style="color:#93C800">tusendel</span></strong> och därmed värdet <math> \, {\color{LimeGreen} 8} \cdot 0,001 \, = \, {\color{Red}{0,008}} \, </math>. |
Summerar man alla decimalers värden beräknas decimaltalets värde till: | Summerar man alla decimalers värden beräknas decimaltalets värde till: | ||
Versionen från 12 juli 2015 kl. 11.00
| <-- Förra avsnitt | Genomgång | Övningar | Nästa avsnitt --> |
Tal mellan två heltal
För att visa tal som ligger mellan två heltal fortsätter man med det decimala positionssystemet.
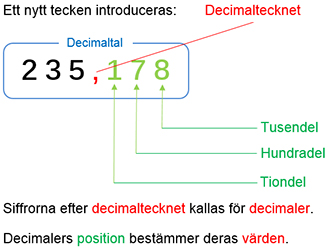
Decimaltecknet lägger till heltalet \( \, 235 \, \) några bråkdelar av en hel etta genom att placera siffror efter decimaltecknet.
På så sätt hamnar talets värde mellan heltalen \( \, 235 \, \) och \( \, 236 \).
Exempel 1
Bestäm decimalernas värden i decimaltalet \( \, 235{\bf{\color{Red},}}{\color{LimeGreen} {178}} \, \). Beräkna decimaltalets värde utgående från decimalernas värden.
Lösning:
- Första decimalen \( \, {\color{LimeGreen} 1} \, \) har positionen tiondel och därmed värdet \( \, {\color{LimeGreen} 1} \cdot 0,1 \, = \, {\color{Red}{0,1}} \).
- Andra decimalen \( \, {\color{LimeGreen} 7} \, \) har positionen hundradel och därmed värdet \( \, {\color{LimeGreen} 7} \cdot 0,01 \, = \, {\color{Red}{0,07}} \, \).
- Tredje decimalen \( \, {\color{LimeGreen} 8} \, \) har positionen tusendel och därmed värdet \( \, {\color{LimeGreen} 8} \cdot 0,001 \, = \, {\color{Red}{0,008}} \, \).
Summerar man alla decimalers värden beräknas decimaltalets värde till:
- \[ 235 \quad {\bf{\color{Red}+}} \quad {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} \; = \; 235{\bf{\color{Red},}}{\color{LimeGreen} {178}} \]