Skillnad mellan versioner av "4.8 Beräkningar med funktioner"
Taifun (Diskussion | bidrag) m (→Exempel Vinternatt) |
Taifun (Diskussion | bidrag) m (→Exempel Vinternatt) |
||
| Rad 64: | Rad 64: | ||
:::::'''kl 2 kl 5 kl 7''' | :::::'''kl 2 kl 5 kl 7''' | ||
| − | b) | + | b) Jämför resultaten i a) med grafen till <math> \, y \, = \, f(x) \, </math>.</td> |
| + | |||
| + | b) Avläs vinternattens lägsta temperatur från grafen. När inträffar den? | ||
| + | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Versionen från 21 mars 2020 kl. 16.49
| << Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
Exempel på funktioner
\[ y \, = \, f(x) \, = \, 4\,x + 12 \]
\[ y \, = \, g(x) \, = \, 3\,x^2 + 5\,x - 16 \]
\[ y \, = \, h(x) \, = \, 8\,x^3 - 4\,x\]
En funktions värde
En funktion definieras med ett uttryck, liknande en formel.
Därför är funktionens värde uttryckets värde.
En funktion har inget givet värde för sig utan får ett värde för något specificerat värde för \(\,x\,\).
Exempel: Beräkna följande funktions värde för \( \, x = 0,5 \, \):
- \[ y \, = \, h(x) \, = \, 8\,x^3 - 4\,x \]
Lösning: Vi sätter in \( 0,5\,\) för \(x\,\) i funktionen för att beräkna funktionens värde:
- \[ 8 \cdot 0,5^3 - 4 \cdot 0,5 = 8 \cdot 0,125 - 2 = 1 - 2 = -1 \,\]
Den givna funktionens värde för \( \, x = 0,5\, \) är \( \, -1\,\). Man skriver \( \, h(0,5) \, = \, -1\,\).
För andra värden på \(\,x\,\) kommer funktionen att ha andra värden.
Exempel Vinternatt
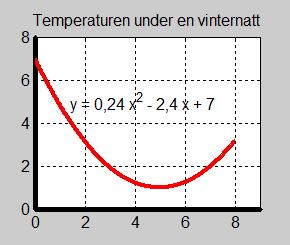 |
Under en vinternatt varierar temperaturen enligt funktionen:
\( x \;\, = \) tiden i timmar efter midnatt a) Bestäm vinternattens temperatur algebraiskt vid:
|
b) Avläs vinternattens lägsta temperatur från grafen. När inträffar den?
</td>