Skillnad mellan versioner av "1.3 Decimaltal+"
Taifun (Diskussion | bidrag) m (→Exempel 2) |
Taifun (Diskussion | bidrag) m |
||
| Rad 24: | Rad 24: | ||
| − | <div class="tolv"> <!-- | + | <div class="tolv"> <!-- tolv1 --> |
Heltalsdelen <math> \, 235</math>:s decimala positionsutveckling visades i avsnittet [[1.1_Om_tal#Det_decimala_positionssystemet|<strong><span style="color:blue">Om tal</span></strong>]]. | Heltalsdelen <math> \, 235</math>:s decimala positionsutveckling visades i avsnittet [[1.1_Om_tal#Det_decimala_positionssystemet|<strong><span style="color:blue">Om tal</span></strong>]]. | ||
| Rad 30: | Rad 30: | ||
På så sätt hamnar talets värde mellan heltalen <math> \, 235 \, </math> och <math> \, 236 </math>. | På så sätt hamnar talets värde mellan heltalen <math> \, 235 \, </math> och <math> \, 236 </math>. | ||
| − | </div> <!-- | + | </div> <!-- tolv1 --> |
| Rad 52: | Rad 52: | ||
| − | <div class="tolv"> <!-- | + | <div class="tolv"> <!-- tolv2 --> |
Samma [[1.1_Om_tal#Exempel_1|<strong><span style="color:blue">regel</span></strong>]] som gällde för heltal, gäller för decimaltal, fast lite annorlunda formulerad: | Samma [[1.1_Om_tal#Exempel_1|<strong><span style="color:blue">regel</span></strong>]] som gällde för heltal, gäller för decimaltal, fast lite annorlunda formulerad: | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
I det decimala positionssystemet har varje position ett <math> \, 10 \, </math> gånger <span style="color:red">mindre värde</span> än positionen till <span style="color:red">vänster</span>. | I det decimala positionssystemet har varje position ett <math> \, 10 \, </math> gånger <span style="color:red">mindre värde</span> än positionen till <span style="color:red">vänster</span>. | ||
</div> | </div> | ||
| − | </div> <!-- | + | </div> <!-- tolv2 --> |
| Rad 74: | Rad 74: | ||
</big></div> <!-- exempel2 --> | </big></div> <!-- exempel2 --> | ||
| − | Detta är ett exempel på att alla heltal | + | <div class="tolv"> <!-- tolv3 --> |
| + | Detta är ett exempel på att alla heltal även är decimaltal, för mängden av alla heltal är en delmängd av alla decimaltal (jfr. med bilden i [[1.1_Om_tal#Olika_typer_av_tal|<strong><span style="color:blue">Olika typer av tal</span></strong>]]). | ||
| + | </div> <!-- tolv3 --> | ||
Versionen från 12 juli 2015 kl. 19.27
| <-- Förra avsnitt | Genomgång | Övningar | Nästa avsnitt --> |
Tal mellan två heltal
För att visa tal som ligger mellan två heltal fortsätter man med det decimala positionssystemet.
Heltalsdelen \( \, 235\):s decimala positionsutveckling visades i avsnittet Om tal.
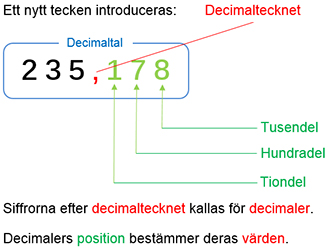
Decimaltecknet lägger till denna heltalsdel några bråkdelar av \( \, 1 \), genom att placera några siffror efter decimaltecknet.
På så sätt hamnar talets värde mellan heltalen \( \, 235 \, \) och \( \, 236 \).
Exempel 1
Bestäm decimalernas värden i decimaltalet \( \, 235{\bf{\color{Red},}}{\color{LimeGreen} {178}} \, \). Beräkna decimaltalets värde utgående från decimalernas värden.
Lösning:
- Första decimalen \( \, {\color{LimeGreen} 1} \, \) har positionen tiondel och därmed värdet \( \, {\color{LimeGreen} 1} \cdot 0,1 \, = \, {\color{Red}{0,1}} \).
- Andra decimalen \( \, {\color{LimeGreen} 7} \, \) har positionen hundradel och därmed värdet \( \, {\color{LimeGreen} 7} \cdot 0,01 \, = \, {\color{Red}{0,07}} \, \).
- Tredje decimalen \( \, {\color{LimeGreen} 8} \, \) har positionen tusendel och därmed värdet \( \, {\color{LimeGreen} 8} \cdot 0,001 \, = \, {\color{Red}{0,008}} \, \).
Summerar man alla decimalers värden beräknas decimaltalets värde till:
- \[ 235 \quad {\bf{\color{Red}+}} \quad {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} \; = \; 235{\bf{\color{Red},}}{\color{LimeGreen} {178}} \]
Samma regel som gällde för heltal, gäller för decimaltal, fast lite annorlunda formulerad:
I det decimala positionssystemet har varje position ett \( \, 10 \, \) gånger mindre värde än positionen till vänster.
Exempel 2
Är \( \, 7\,142 \, \) ett heltal eller ett decimaltal?
Svar:
- \( \, 7\,142 \, \) är både heltal och decimaltal.
- Heltal, därför att det inte finns något decimaltecken i det.
- Decimaltal, därför att man kan skriva: \( \qquad 7\,142 \; = \; 7\,142 \, {\bf{\color{Red},}} \, {\color{LimeGreen} {000\, \ldots}} \)
Detta är ett exempel på att alla heltal även är decimaltal, för mängden av alla heltal är en delmängd av alla decimaltal (jfr. med bilden i Olika typer av tal).