Skillnad mellan versioner av "1.3 Decimaltal+"

Versionen från 15 juli 2015 kl. 14.31

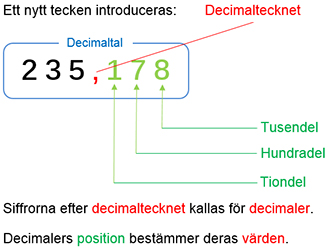
Tal mellan två heltal

För att visa tal som ligger mellan två heltal fortsätter man med det decimala positionssystemet.

Heltalsdelen \( 235\):s framställning i det decimala positionssystemet förklarades i avsnittet Om tal, Exempel 1 (\( \, 7\,142 \)).

Till denna heltalsdel lägger man efter decimaltecknet några bråkdelar av \( \, 1 \), dvs decimalerna \( \, \ldots{\bf{\color{Red},}}{\color{LimeGreen} {178}} \, \).

På så sätt hamnar talets värde mellan heltalen \( \, 235 \, \) och \( \, 236 \).

Exempel 1

Bestäm decimalernas värden i decimaltalet \( \, 235{\bf{\color{Red},}}{\color{LimeGreen} {178}} \, \). Beräkna decimaltalets värde utgående från decimalernas värden.

Lösning:

Första decimalen \( \, {\color{LimeGreen} 1} \, \) har positionen tiondel och därmed värdet \( \, {\color{LimeGreen} 1} \cdot 0,1 \, = \, {\color{Red}{0,1}} \).

Andra decimalen \( \, {\color{LimeGreen} 7} \, \) har positionen hundradel och därmed värdet \( \, {\color{LimeGreen} 7} \cdot 0,01 \, = \, {\color{Red}{0,07}} \, \).

Tredje decimalen \( \, {\color{LimeGreen} 8} \, \) har positionen tusendel och därmed värdet \( \, {\color{LimeGreen} 8} \cdot 0,001 \, = \, {\color{Red}{0,008}} \, \).

Summerar man alla decimalers värden beräknas decimaltalets värde till:

\[ 235 \quad {\bf+} \quad {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} \quad = \quad 235\,{\bf{\color{Red},}}\,{\color{LimeGreen} {178}} \]

Samma regel som gällde för heltal, gäller för decimaltal, fast lite annorlunda formulerad:

I det decimala positionssystemet har varje position ett \( \, 10 \, \) gånger mindre värde än positionen till vänster.

Om decimaltal ligger mellan två heltal, hur ligger det till med heltalen själva?

Exempel 2

Är \( \, 7\,142 \, \) ett heltal eller ett decimaltal? Motivera.

Svar:

\( \, 7\,142 \, \) är både heltal och decimaltal.

Heltal, därför att det inte finns något decimaltecken i det.

Decimaltal, därför att man kan sätta ett decimaltecken och skriva: \( \qquad 7\,142 \; = \; 7\,142 \, {\bf{\color{Red},}} \, {\color{LimeGreen} {000\, \ldots}} \)

Detta är ett exempel på att alla heltal även är decimaltal, för till alla heltal kan ett decimaltecken tillfogas som följs av nollor.

Dessutom är mängden av alla heltal en delmängd av alla decimaltal, se bilden i Olika typer av tal, där decimaltal \( \, = \, \) rationella & reella tal.

Exempel 2 visar också:

Alla nollor efter decimaltecknet kan utelämnas, om ingen siffra \( \neq 0 \, \) finns efter nollorna.

Anledningen till denna regel är att sådana nollor efter decimaltecknet inte bidrar något (eller bidrar värdet \( \, 0 \)) till decimaltalets värde.

Placering av decimaltal på tallinjen

Kunskapen om decimaltalens värde ska hjälpa oss att ha en uppfattning om decimaltalens storlek och deras korrekta placering på tallinjen.

Exempel 3

Vilket decimaltal pekar pilen på? \(\quad \)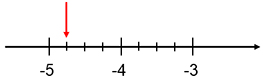

Lösning:

Fil:Decimaltallinje Svar 60.jpg

Förklaring:

Vi befinner oss på den negativa delen av tallinjen.
Skalans minsta steg på tallinjen är: \( \; 1 \,/\, 4 \, = \, \displaystyle{{1 \over 4} \, = \, {1 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \, = \, {5 \over 20} \, = \, {5 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \, = \, {25 \over 100}} \, = \, 0,25 \)
Det sökta decimaltalet ligger mellan heltalen \( \, -4 \, \) och \( \, -5 \).
Utgående från \( \, -4 \, \) rör vi oss tre steg till vänster för att hitta det sökta decimaltalet: \( \, -4 \,-\, 0,25 \,-\, 0,25 \,-\, 0,25 \, = \, {\color{Red} {-4,75}}\).

Omvandlingen av \( \, 1 \,/\, 4 \, \) till \( \, 0,25 \, \) i förklaringen ovan är ett exempel på användningen av viktiga decimaltal. Här sammanfattas några:

Viktiga decimaltal

\[ \displaystyle{ 0,1 \, = \, {1 \over 10} } \]

\[ \displaystyle{ 0,01 \, = \, {1 \over 100} } \]

\[ \displaystyle{ 0,001 \, = \, {1 \over 1000} } \]

\[ \displaystyle{ 0,5 \, = \, {1 \over 2} } \]

\[ \displaystyle{ 0,25 \, = \, {1 \over 4} } \]

\[ \displaystyle{ 0,75 \, = \, {3 \over 4} } \]

\[ \displaystyle{ 0,333\,333\,\ldots \, = \, {1 \over 3} } \]

\[ \displaystyle{ 0,666\,666\,\ldots \, = \, {2 \over 3} } \]

\[ \displaystyle{ 0,111\,111\,\ldots \, = \, {1 \over 9} } \]

\[ \pi \quad = \, 3,141592653589793\,\ldots \]

\[ \sqrt{2} \, = \, 1,414213562373095\,\ldots \]

\[ \sqrt{3} \, = \, 1,732050807568877\,\ldots \]

I exemplen ovan kan man skilja åt tre grupper:

Decimaltal med s.k. ändlig decimalutveckling, t.ex. \( \, 0,75 \, \).
Decimaltal med s.k. periodisk decimalutveckling, t.ex. \( \, 333\,333\,\ldots \, \).
Decimaltal med s.k. icke-periodisk decimalutveckling, t.ex. \( \, 3,141592653589793\,\ldots \, \).

De två första grupperna bildar de rationella talen, medan den tredje gruppen tillhör de reella talen, se Olika typer av tal.

Alla ändliga och periodiska decimalutvecklingar kan man skriva i bråkform (rationella), medan det inte längre går med de icke-periodiska (reella).

Ändlig decimalutveckling

Så kallas decimaltal med ändligt många decimaler \(-\) den vanligaste typen av decimaltal \(-\) om man följer den redan nämnda regeln att utelämna nollorna efter decimaltecknet, t.ex. \( \,0,75\,000\,000\,\ldots \, = \, 0,75 \, \).

Ändliga decimalutvecklingar skrivs om till bråk med en \( \, 10\)-potens (en \( \, 1 \, \) med nollor) i nämnaren och förkortas så långt som möjligt.

Exempel 4

a) Skriv \( \; 0,75 \; \) i bråkform.

Lösning: \( \; 0,75 \, = \, \displaystyle{{75 \over 100} \, = \, {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \, = \, {3 \cdot {\color{Red} {5 \cdot 5}} \over 4 \cdot {\color{Red} {5 \cdot 5}}} \, = \, {3 \cdot \cancel{\color{Red} {5 \cdot 5}} \over 4 \cdot \cancel{\color{Red} {5 \cdot 5}}} \, = \, {3 \over 4} } \)

b) Skriv \( \; \displaystyle{3 \over 4} \; \) till decimaltal.

Lösning: \( \; \displaystyle{{3 \over 4} \, = \, {3 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \, = \, {15 \over 20} \, = \, {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \, = \, {75 \over 100}} \, = \, 0,75 \)

För att skriva bråk till decimaltal förlängs bråket så länge tills en \( \, 10\)-potens i nämnaren tillåter ändlig decimalutveckling.

Exempel 5

a) Skriv \( \; 0,125 \; \) i bråkform.

Lösning: \( \; 0,125 \, = \, \displaystyle{{125 \over 1000} \, = \, {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \, = \, {5 \cdot {\color{Red} {5 \cdot 5}} \over 40 \cdot {\color{Red} {5 \cdot 5}}} \, = \, {1 \cdot {\color{Red} {5 \cdot 5 \cdot 5}} \over 8 \cdot {\color{Red} {5 \cdot 5 \cdot 5}}} \, = \, {1 \cdot \cancel{\color{Red} {5 \cdot 5 \cdot 5}} \over 8 \cdot \cancel{\color{Red} {5 \cdot 5 \cdot 5}}} \, = \, {1 \over 8} } \)

b) Skriv \( \; \displaystyle{1 \over 8} \; \) till decimaltal.

Lösning: \( \; \displaystyle{{1 \over 8} \, = \, {1 \cdot {\color{Red} 5} \over 8 \cdot {\color{Red} 5}} \, = \, {5 \over 40} \, = \, {5 \cdot {\color{Red} 5} \over 40 \cdot {\color{Red} 5}} \, = \, {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \, = \, {125 \over 1000}} \, = \, 0,125 \)

@@ Rad 176: / Rad 176: @@
 Så kallas decimaltal med ändligt många decimaler <math>-</math> den vanligaste typen av decimaltal <math>-</math> om man följer den redan nämnda [[1.3 Decimaltal#Exempel_2|<strong><span style="color:blue">regeln</span></strong>]] att utelämna nollorna efter decimaltecknet, t.ex. <math> \,0,75\,000\,000\,\ldots \, = \, 0,75 \, </math>.
-Ändliga decimalutvecklingar skrivs i bråkform med en <math> \, 10</math>-potens i nämnaren och förkortas så långt som möjligt.
+Ändliga decimalutvecklingar skrivs om till bråk med en <math> \, 10</math>-potens (en <math> \, 1 \, </math> med nollor) i nämnaren och förkortas så långt som möjligt.
 </div> <!-- tolv6 -->