Skillnad mellan versioner av "1.7 Lathund till Potenser Appversion"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 55: | Rad 55: | ||
<b><span style="color:#931136">Lagen om negativ exponent:</span></b> | <b><span style="color:#931136">Lagen om negativ exponent:</span></b> | ||
<br> | <br> | ||
| − | <big><math> \qquad\qquad\qquad\; a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad </math></big> | + | <big><math> \qquad\qquad\qquad\;\, a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad </math></big> |
---- | ---- | ||
<b><span style="color:#931136">Potens av en produkt:</span></b> | <b><span style="color:#931136">Potens av en produkt:</span></b> | ||
Versionen från 19 mars 2016 kl. 20.16
| Genomgång Potenser | Genomgång Grundpotensform | Quiz | Övningar | Lathund Webb |
| Genomgång Potenser | Genomgång Grundpotensform | Övningar App spår 1 | Övningar App spår 1 | Lathund App |
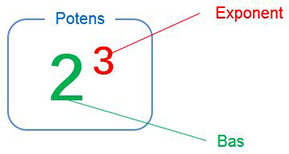
Potens
Ex.:
- \[ 2\,^{\color{Red} 3} \; = \;\; \underbrace{2 \, \cdot \, 2 \, \cdot \, 2}_{{\color{Red} 3}\;\times} \]
Potens = upprepad multiplikation
av \( \, 2 \, \) med sig själv, \( \, {\color{Red} 3} \, \) gånger.
Potenslagarna
Första potenslagen:
\( \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad \)
Andra potenslagen:
\( \qquad\qquad\qquad\;\;\, \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad \)
Tredje potenslagen:
\( \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad \)
Lagen om nollte potens:
\( \qquad\qquad\qquad\quad a\,^0 \; = \; 1 \qquad \)
Lagen om negativ exponent:
\( \qquad\qquad\qquad\;\, a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad \)
Potens av en produkt:
\( \qquad\qquad\;\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad \)
Potens av en kvot:
\( \qquad\qquad\quad\; \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad \)
Grundpotensform
Definition:
- \[ a \, \cdot \, 10\,^n \quad\; {\rm kallas\;\;{\color{Red} {grundpotensform}}} \]
- \[ {\rm om} \;\; n \;\; {\rm är\;\;heltal} \quad\; {\rm och} \quad\; 1 \leq a < 10 \; {\rm .} \]
Copyright © 2010-2016 Math Online Sweden AB. All Rights Reserved.