Skillnad mellan versioner av "3.3 Ekvationer 2 kolumner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 60: | Rad 60: | ||
endast en obekant. <math> \qquad\;\, </math> Ex. ovan<span style="color:black">:</span> | endast en obekant. <math> \qquad\;\, </math> Ex. ovan<span style="color:black">:</span> | ||
| + | |||
| + | Ekvationens <b><span style="color:#931136">lösning:</span></b> <math> \quad\; </math> <div class="smallBoxVariantt"> <math> x \; = \; {\color{Red} 2} </math></div> | ||
Ekvationens <b><span style="color:#931136">lösning:</span></b> <math> \quad\; </math> <div class="smallBoxVariantt"> <math> x \; = \; {\color{Red} 2} </math></div> | Ekvationens <b><span style="color:#931136">lösning:</span></b> <math> \quad\; </math> <div class="smallBoxVariantt"> <math> x \; = \; {\color{Red} 2} </math></div> | ||
Versionen från 9 maj 2016 kl. 22.08
| Genomgång | Potensekvationer | Quiz | Övningar | Lathund |
Varför ekvationer? \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Exempel på en ekvation
Uppgift:
Lösning med ekvation: \( \quad\;\; x \; = \; {\rm flaskans\;pris} \)
|
\( \qquad\qquad \) | \( \qquad \)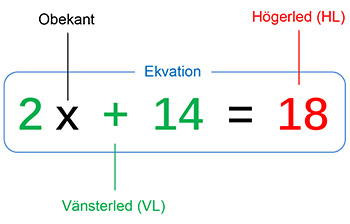
Ekvation \( \; = \; \) En likhet mellan två uttryck. Innehåller alltid ett likhetstecken och endast en obekant. \( \qquad\;\, \) Ex. ovan: Ekvationens lösning: \( \quad\; \) \( x \; = \; {\color{Red} 2} \)
Ekvationens lösning: \( \quad\; \) \( x \; = \; {\color{Red} 2} \)
Kontroll: Sätt in lösningen i ekvationen. VL \( \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 \) HL \( \, = \, 18 \) VL \( \; = \; \) HL \( \qquad \Rightarrow \qquad \) OK \( \qquad\; \) Kontroll kallas ibland för prövning. |
Obekanta är variabler som förekommer i ekvationer. Ofta används bokstaven \( \, x \, \) för obekanta. Men det är inget måste.
Variabler är bokstäver eller platshållare för tal. De namnges med bokstäver, som lådor med etiketter. Innehållet är tal och kallas för variabelns värde.
Uttryck är en kombination av variabler, tal, räkneoperationer och parenteser som till slut, när uttrycket beräknas, ger ett värde. Inte alla ingredienser behöver ingå i ett uttryck, se avsnitt 3.1 Uttryck.
Formel är en likhet mellan två uttryck med minst två variabler, se avsnitt 3.5 Formler.
+++
\( \, 2\,^3 \, \) läses \( \, {\color{Red} 2} \) upphöjt till\( \, {\color{Red} 3} \, \) och kallas för potens. \( \, 2\, \) heter basen och \( \, 3 \, \) exponenten.
Exponenten \( \, {\color{Red} 3} \, \) är inget tal i vanlig bemärkelse utan endast en information om att \( \, 2 \, \) ska multipliceras \( \, {\color{Red} 3} \, \) gånger med sig själv (jfr. upprepad addition).
Exempel 1
Förenkla: \( \qquad \displaystyle{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \)
Lösning: \( \qquad \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \over 2 \cdot 2 \cdot 2 \cdot 2} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot \cancel{2 \cdot 2 \cdot 2 \cdot 2} \over \cancel{2 \cdot 2 \cdot 2 \cdot 2}} \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} \)
- OBS! Förenkla alltid först, räkna sedan!
Snabbare: \( \qquad\!\! \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, 2\,^{3\,+\,5\,-\,4} \, = \, 2\,^4 \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} \)
För att förstå den snabbare lösningen se potenslagarna.
Potens med positiva heltalsexponenter
Potensen \( \, a\,^{\color{Red} x} \, \) kan, om exponenten \( \, {\color{Red} x} \, \) är ett positivt heltal och basen \( \, a \, \) ett tal \( \neq 0 \), definieras som
- Upprepad multiplikation av \( \, a \, \) med sig själv, \( \, {\color{Red} x} \, \) gånger:
- \( a\,^{\color{Red} x} = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{{\color{Red} x}\;{\rm gånger}} \)
Exempel 2
Förenkla: \( \quad\;\; a\,^2 \, \cdot \, a\,^3 \)
Lösning:
- \( a\,^2 \cdot a\,^3 \; = \; \underbrace{a \cdot a}_{2\;\times} \; \cdot \; \underbrace{a \cdot a \cdot a}_{3\;\times} \; = \; \underbrace{a \cdot a \cdot a \cdot a \cdot a}_{{\color{Red} 5}\;\times} \; = \; a\,^{\color{Red} 5}\)
Snabbare:
- \( a\,^2 \cdot a\,^3 \; = \; a\,^{2\,+\,3} = \; a\,^{\color{Red} 5} \)
Den snabbare lösningen är ett exempel på den första potenslagen:
Potenslagarna
Följande lagar gäller för potenser där basen \( a\, \) är ett tal \( \neq 0 \), exponenterna \( \, x \, \) och \( \, y \, \) godtyckliga tal och \( m,\,n \) heltal (\( n\neq 0 \)):
Första potenslagen: \( \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad \)
Andra potenslagen: \( \qquad\qquad\qquad\;\;\; \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad \)
Tredje potenslagen: \( \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad \)
Lagen om nollte potens: \( \qquad\qquad\quad\;\;\, a\,^0 \; = \; 1 \qquad\qquad \)
Lagen om negativ exponent: \( \qquad\quad\;\;\; a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad \)
Potens av en produkt: \( \qquad\qquad\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad \)
Potens av en kvot: \( \qquad\qquad\qquad\, \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad \)
För enkelhets skull definierades potensbegreppet inledningsvis endast för positiva heltalsexponenter \( \, x \, \) och \( \, y \). Men potenslagarna gäller även för exponenter som är negativa eller bråktal. I formuleringen "negativ exponent" antas \( \, x > 0 \).
Exempel 3
- \( \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; {a \cdot a \cdot a \cdot a \cdot a \; \over \; a \cdot a \cdot a} \; = \; {a \cdot a \cdot \cancel{a \cdot a \cdot a} \; \over \; \cancel{a \cdot a \cdot a}} \; = \; a \cdot a \; = \; a\,^2 \)
Snabbare med andra potenslagen:
- \( \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5\,-\,3}}} \; = \; a\,^2 \)
Påstående (Lagen om nollte potens):
- \( a^0 \; = \; 1 \)
Bevis:
Påståendet kan bevisas genom att använda andra potenslagen:
- \( \displaystyle{a^x \over a^x} \; = \; a^{x-x} \; = \; a^0 \)
Å andra sidan vet vi att ett bråk med samma täljare som nämnare har värdet \( \, 1 \):
- \( \displaystyle{a^x \over a^x} \; = \; 1 \)
Av raderna ovan följer påståendet:
- \( a^0 \; = \; 1 \)
Exempel på potenser med negativa exponenter
- \[ \displaystyle{10\,^{-1} \, = \, {1 \over 10\,^1} \, = \, {1 \over 10} \, = \, 0,1} \]
- \[ \displaystyle{10\,^{-2} \, = \, {1 \over 10\,^2} \, = \, {1 \over 10 \cdot 10} \, = \, {1 \over 100} \, = \, 0,01} \]
- \[ \displaystyle{10\,^{-3} \, = \, {1 \over 10\,^3} \, = \, {1 \over 10 \cdot 10 \cdot 10} \, = \, {1 \over 1000} \, = \, 0,001} \]
Påstående (Lagen om negativ exponent, \( \, x > 0 \)):
- \( a^{-x} = \displaystyle{1 \over a^x} \)
Bevis:
Påståendet kan bevisas genom att använda lagen om nollte potensen (baklänges) samt andra potenslagen:
- \( \displaystyle{1 \over a^x} \; = \; \displaystyle{a^0 \over a^x} \; = \; a^{0-x} \; = \; a^{-x} \)
Vi får påståendet, fast baklänges.
Att potenser med negativa exponenter är en naturlig fortsättning på potenser med positiva exponenter med nollte potensen däremellan illustrerar följande exempel:
Varför är \( \; 5\,^0 \, = \, 1 \; \)?
- \[ \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 \]
- \[ \;\; 5^3 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \]
- \[ \;\; 5^2 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \]
- \[ \;\; 5^1 \; = \; {\color{Red} 1} \cdot 5 \]
- \[ \;\; {\color{Red} {5^0 \; = \; 1}} \]
- \[ \;\; 5^{-1} \; = \; \displaystyle{{\color{Red} 1} \over 5} \]
- \[ \;\; 5^{-2} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5} \]
- \[ \;\; 5^{-3} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5} \]
- \[ \;\; 5^{-4} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5 \cdot 5 } \]
Att \( \; {\color{Red} 1} \)-orna följer med hela tiden beror på att multiplikationens enhet är \( \, {\color{Red} 1} \), dvs \( \, a \cdot {\color{Red} 1} \, = \, a \). Därför blir endast \( \, {\color{Red} 1} \, \) kvar, när vi kommer till \( \, {\color{Red} {5^0}} \, \) då alla \( \, 5\)-or har försvunnit.
Jämför med:
Varför är \( \; 5 \cdot 0 \, = \, 0 \; \)?
- \[ \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 \]
- \[ \;\; 5 \cdot 3 \; = \; {\color{Red} 0} + 5 + 5 + 5 \]
- \[ \;\; 5 \cdot 2 \; = \; {\color{Red} 0} + 5 + 5 \]
- \[ \;\; 5 \cdot 1 \; = \; {\color{Red} 0} + 5 \]
- \[ \;\; {\color{Red} {5 \cdot 0 \; = \; 0}} \]
- \[ \;\; 5 \cdot (-1) \; = \; {\color{Red} 0} - 5 \]
- \[ \;\; 5 \cdot (-2) \; = \; {\color{Red} 0} - 5 - 5 \]
- \[ \;\; 5 \cdot (-3) \; = \; {\color{Red} 0} - 5 - 5 - 5 \]
- \[ \;\; 5 \cdot (-4) \; = \; {\color{Red} 0} - 5 - 5 - 5 - 5 \]
Att \( \; {\color{Red} 0} \)-orna följer med hela tiden beror på att additionens enhet är \( \, {\color{Red} 0} \), dvs \( \, a + {\color{Red} 0} \, = \, a \). Därför blir endast \( \, {\color{Red} 0} \, \) kvar, när vi kommer till \( \, {\color{Red} {5 \cdot 0}} \, \) då alla \( \, 5\)-or har försvunnit.
Internetlänkar
https://www.youtube.com/watch?v=BMEOkzq3Xo4
http://www.youtube.com/watch?v=iYgG4LUqXks
http://www.webbmatte.se/gym/arabiska/2/2_8_4sv.html
http://www.webbmatte.se/gym/arabiska/2/2_8_3sv.html
Copyright © 2010-2016 Math Online Sweden AB. All Rights Reserved.