Skillnad mellan versioner av "3.3 Ekvationer 2 kolumner"

Från Mathonline
Hoppa till: navigering, sök
m
m
Rad 90: Rad 90:
  
  
 +
== <b><span style="color:#931136">Ekvationslösning med inspektionsmetoden</span></b> ==
  
 +
<br>
  
 +
<div class="border-divblue">
 +
<big><b><span style="color:#931136">Exemplet ovan:</span></b>
  
 +
&nbsp; <math> 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x </math>
  
 +
<div class="RedBox2x"><math>\quad</math></div> <math> \, + \;\, 14 \; = \; 18 </math>
  
 +
&nbsp; <math> \;\, 4 \;\;\; + \; 14 \; = \; 18 </math>
  
 +
&nbsp; <math> \;\, \Downarrow </math>
  
 +
&nbsp; <math> \, {\color{Red} {2 \, \cdot \; x}} \;\; = \;\, 4  \qquad\quad {\color{Red} {{\rm Täck\;över\;} x}}</math>
  
 +
&nbsp; <math> \, 2 \, \cdot \; </math><div class="RedBoxx"><math> \quad </math></div> <math> \; = \;\, 4 </math>
  
 +
&nbsp; <math> \, 2 \, \cdot \; 2 \;\; = \;\; 4 </math>
  
−
+++
+
&nbsp; <math> \quad\;\;\; \Downarrow </math>
  
−
<div class="tolv"> <!-- tolv2 -->
+
&nbsp; <div class="smallBoxVariantt"> <math> \; {\color{Red} x} \; = \; 2 </math></div>
−
<math> \, 2\,^3 \, </math> läses <math> \, {\color{Red} 2} </math> <strong><span style="color:red">upphöjt till</span></strong><math> \, {\color{Red} 3} \, </math> och kallas för &nbsp;<strong><span style="color:red">potens</span></strong>. <math> \, 2\, </math> heter <strong><span style="color:red">basen</span></strong> och <math> \, 3 \, </math> <strong><span style="color:red">exponenten</span></strong>.
+
</big></div>
  
−
Exponenten <math> \, {\color{Red} 3} \, </math> är inget tal i vanlig bemärkelse utan endast en information om att <math> \, 2 \, </math> ska multipliceras <math> \, {\color{Red} 3} \, </math> gånger med sig själv  (jfr. [[1.2_Räkneordning#Varf.C3.B6r_g.C3.A5r_multiplikation_f.C3.B6re_addition.3F|<strong><span style="color:blue">upprepad addition</span></strong>]]).
 
−
</div> <!-- tolv2 -->
 
  
 +
== <b><span style="color:#931136">Ekvationslösning med allmän metod</span></b> ==
  
−
<div class="exempel"> <!-- exempel1 -->
+
<br>
−
== <b><span style="color:#931136">Exempel 1</span></b> ==
+
−
<big>
+
−
Förenkla<span style="color:black">:</span> <math> \qquad \displaystyle{2\,^3 \cdot \; 2\,^5 \over 2\,^4} </math>
+
  
 +
<div class="ovnE">
 +
<big><b><span style="color:#931136">Exemplet ovan:</span></b></big>
  
−
<strong><span style="color:#931136">Lösning:</span></strong> <math> \qquad \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \over 2 \cdot 2 \cdot 2 \cdot 2} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot \cancel{2 \cdot 2 \cdot 2 \cdot 2} \over \cancel{2 \cdot 2 \cdot 2 \cdot 2}} \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} </math>
+
<div class="exempel">
 +
::<math>\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18                                        &          &                        \\
 +
                              x \, + \, x \, + \, 14 & = & 18                                        &          &                        \\
 +
                                      2\,x \, + \, 14 & = & 18                                        & \qquad | & {\color{Red} {- \, 14}} \\
 +
          2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}}            &          &                        \\
 +
                                      2\,x \,        & = & 4                                        & \qquad | & {\color{Red} {/ \; 2}}  \\
 +
        \displaystyle \frac{2\,x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} &          &                        \\
 +
                                        x \,         & = & 2                                        &          &
 +
          \end{array}</math>
 +
</div>
  
−
:::::::::::::::::OBS! &nbsp; Förenkla alltid först, räkna sedan!
+
Skrivsättet <math> \quad | \quad {\color{Red} {- \, 14}} \quad\!</math> är en kortform på<span style="color:black">:</span>
  
−
Snabbare<span style="color:black">:</span> <math> \qquad\!\! \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, 2\,^{3\,+\,5\,-\,4} \, = \, 2\,^4 \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} </math>
+
::::Subtrahera <math> \, 14 \, </math> från ekvationens båda led.
−
</big>
+
−
</div>  <!-- exempel1 -->
+
  
 +
Skrivsättet <math> \quad | \quad {\color{Red} {/ \; 2}} \quad\;\; </math> är en kortform på<span style="color:black">:</span>
  
−
<div class="tolv"> <!-- tolv2 -->
+
::::Dividera ekvationens båda led med <math> \, 2 </math>.
−
För att förstå den snabbare lösningen se [[1.7_Potenser#Potenslagarna|<strong><span style="color:blue">potenslagarna</span></strong>]].
+
</div>
−
</div> <!-- tolv2 -->
+
  
  
−
== <b><span style="color:#931136">Potens med positiva heltalsexponenter</span></b> ==
+
:<big><b>God redovisningsstil:</b>  
−
<div class="tolv"> <!-- tolv1 -->
+
  
−
Potensen <big><math> \, a\,^{\color{Red} x} \, </math></big> kan, om exponenten <math> \, {\color{Red} x} \, </math> är ett positivt heltal och basen <big><math> \, a \, </math></big> ett tal <math> \neq 0 </math>, definieras som
+
*&nbsp;&nbsp; Skriv likhetstecknen exakt under varandra (samma kolumn).
  
−
::::::<b>Upprepad multiplikation av <big><math> \, a \, </math></big> med sig själv, <math> \, {\color{Red} x} \, </math> gånger:</b>
+
*&nbsp;&nbsp; Kommentera, där det behövs, det du gör antingen genom att
  
−
::::::::<big><math> a\,^{\color{Red} x} = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{{\color{Red} x}\;{\rm gånger}} </math></big>
+
:&nbsp;&nbsp; använda skrivsättet i exemplet ovan eller på ditt eget sätt, så
−
</div> <!-- tolv1 -->
+
  
−
<div class="exempel"> <!-- exempel2 -->
+
:&nbsp;&nbsp; att det blir förståeligt vad du gör.
−
== <b><span style="color:#931136">Exempel 2</span></b> ==
+
−
<big>
+
−
Förenkla<span style="color:black">:</span> <big><math> \quad\;\; a\,^2 \, \cdot \, a\,^3 </math></big>
+
  
−
 
+
*&nbsp;&nbsp; Skriv kommentarerna skilda från ekvationens lösningsgång.
−
<strong><span style="color:#931136">Lösning:</span></strong>
+
−
 
+
−
::::<big><math> a\,^2 \cdot a\,^3 \; = \; \underbrace{a \cdot a}_{2\;\times} \; \cdot \; \underbrace{a \cdot a \cdot a}_{3\;\times} \; = \; \underbrace{a \cdot a \cdot a \cdot a \cdot a}_{{\color{Red} 5}\;\times} \; = \; a\,^{\color{Red} 5}</math></big>
+
−
 
+
−
Snabbare:
+
−
 
+
−
::::<big><math> a\,^2 \cdot a\,^3 \; = \; a\,^{2\,+\,3} = \; a\,^{\color{Red} 5} </math></big>
+
 
</big>
 
</big>
−
</div> <!-- exempel2 -->
 
  
  
−
<div class="tolv"> <!-- tolv2 -->
+
<div class="ovnC">
−
Den snabbare lösningen är ett exempel på den första potenslagen:
+
<big><b><span style="color:#931136">Målet:</span></b> <math> \qquad\quad </math> Att <b><span style="color:red">isolera</span></b> <math> \, {\color{Red} x} \, </math> på ett led.</big>
−
</div> <!-- tolv2 -->
+
  
  
−
== <b><span style="color:#931136">Potenslagarna</span></b> ==
+
<big><b><span style="color:#931136">Metoden:</span></b></big>
−
<div class="tolv"> <!-- tolv3 -->
+
  
−
Följande lagar gäller för potenser där basen <math> a\, </math> är ett tal <math> \neq 0 </math>, exponenterna <math> \, x \, </math> och <math> \, y \, </math> godtyckliga tal och <math> m,\,n </math> heltal (<math> n\neq 0 </math>):
 
−
</div> <!-- tolv3 -->
 
  
 +
<b>Steg 1:</b>
 +
<div class="exempel">
  
−
<div class="border-divblue">
+
&nbsp; Förenkla uttrycken i ekvationens båda led så långt som
−
<b><span style="color:#931136">Första potenslagen:</span></b> <big><math> \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Andra potenslagen:</span></b> <big><math> \qquad\qquad\qquad\;\;\; \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Tredje potenslagen:</span></b> <big><math> \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Lagen om nollte potens:</span></b> <big><math> \qquad\qquad\quad\;\;\, a\,^0 \; = \; 1 \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Lagen om negativ exponent:</span></b> <big><math> \qquad\quad\;\;\; a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Potens av en produkt:</span></b> <big><math> \qquad\qquad\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad </math></big>
+
−
----
+
−
<b><span style="color:#931136">Potens av en kvot:</span></b> <big><math> \qquad\qquad\qquad\, \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad </math></big>
+
−
</div> <!-- border-divblue -->
+
  
 +
&nbsp; möjligt: Se de två första raderna i exemplet ovan.
 +
</div>
  
−
<div class="tolv"> <!-- tolv3a -->
 
−
För enkelhets skull definierades potensbegreppet inledningsvis endast för positiva heltalsexponenter <math> \, x \, </math> och <math> \, y </math>. Men potenslagarna gäller även för exponenter som är negativa eller bråktal. I formuleringen "negativ exponent" antas <math> \, x > 0 </math>.
 
−
</div> <!-- tolv3a -->
 
  
 +
<b>Steg 2:</b>
 +
<div class="exempel">
  
−
<div class="exempel"> <!-- exempel3 -->
+
&nbsp; Utför <b><span style="color:red">samma operation</span></b> på ekvationens båda led med må-
−
== <b><span style="color:#931136">Exempel 3</span></b> ==
+
−
<big>
+
  
−
::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; {a \cdot a \cdot a \cdot a \cdot a \; \over \; a \cdot a \cdot a} \; = \; {a \cdot a \cdot \cancel{a \cdot a \cdot a} \; \over \; \cancel{a \cdot a \cdot a}} \; = \; a \cdot a \; = \; a\,^2 </math></big>
+
&nbsp; let att isolera <math> \, x </math>: Se raderna 3 och 5 i exemplet.
  
−
Snabbare med andra potenslagen:
+
&nbsp; <b><span style="color:red">OBS!</span></b> &nbsp;Förenkla under resans gång de nyuppkomna ut-
  
−
::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5\,-\,3}}} \; = \; a\,^2 </math></big>
+
::&nbsp;trycken i ekvationens båda led så långt som möjligt.
−
</big>
+
</div>
−
</div> <!-- exempel3 -->
+
  
  
−
<div class="tolv"> <!-- tolv2 -->
+
<b>Regel: &nbsp;&nbsp; <span style="color:red">Vilken operation?</span> &nbsp;&nbsp; Den som isolerar <math> \, x \, </math>. </b>
−
'''Påstående (Lagen om nollte potens)''':
+
<div class="exempel">
  
−
::::<big><math> a^0 \; = \; 1 </math></big>
+
&nbsp; Rad 3 i exemplet ovan<span style="color:black">:</span>
  
−
'''Bevis''':
+
::::<math> 2\,x \, + \, 14 \; = \; 18 \qquad\quad | \;\; {\color{Red} {- \, 14}} </math>
  
−
Påståendet kan bevisas genom att använda andra potenslagen:
+
&nbsp;<math> \, {\color{Red} {- \, 14}} \, </math> är den <b><span style="color:red">inversa (motsatta) operationen</span></b> till <math> \, + \, 14 \, </math>.
  
−
::::<big><math> \displaystyle{a^x \over a^x} \; = \; a^{x-x} \; = \; a^0 </math></big>
+
&nbsp; Rad 5 i exemplet ovan<span style="color:black">:</span>
  
−
Å andra sidan vet vi att ett bråk med samma täljare som nämnare har värdet <math> \, 1 </math>:
+
:::::<math> \;\; 2 \cdot x \; = \; 4 \qquad\quad\;\; | \;\; {\color{Red} {/ \; 2}} </math>
  
−
::::<big><math> \displaystyle{a^x \over a^x} \; = \; 1 </math></big>
+
&nbsp; Eller<span style="color:black">:</span> <math> \qquad\quad\; x \cdot 2 \; = \; 4 \qquad\quad\;\;\, | \;\; {\color{Red} {/ \; 2}} </math>
  
−
Av raderna ovan följer påståendet:
+
&nbsp; <math> \, {\color{Red} {/ \; 2}} \, </math> är den <b><span style="color:red">inversa operationen</span></b> till <math> \, \cdot \; 2 \, </math>.</div>
  
−
::::<big><math> a^0 \; = \; 1 </math></big>
 
−
</div> <!-- tolv4 -->
 
  
 +
</div>
  
−
<div class="exempel"> <!-- exempel4 -->
 
−
== <b><span style="color:#931136">Exempel på potenser med negativa exponenter</span></b> ==
 
−
<big>
 
  
−
::::<math> \displaystyle{10\,^{-1} \, = \, {1 \over 10\,^1} \, = \, {1 \over 10} \, = \, 0,1} </math>
+
== <b><span style="color:#931136">Ekvationer med obekanten <math> \, x \, </math> i båda leden</span></b> ==
−
 
+
−
::::<math> \displaystyle{10\,^{-2} \, = \, {1 \over 10\,^2} \, = \, {1 \over 10 \cdot 10} \, = \, {1 \over 100} \, = \, 0,01} </math>
+
−
 
+
−
::::<math> \displaystyle{10\,^{-3} \, = \, {1 \over 10\,^3} \, = \, {1 \over 10 \cdot 10 \cdot 10} \, = \, {1 \over 1000} \, = \, 0,001} </math>
+
−
</big>
+
−
</div> <!-- exempel4 -->
+
−
 
+
−
 
+
−
<div class="tolv"> <!-- tolv4a -->
+
−
 
+
−
'''Påstående (Lagen om negativ exponent, <math> \, x > 0 </math>)''':
+
−
 
+
−
::::<big><math> a^{-x} = \displaystyle{1 \over a^x} </math></big>
+
−
 
+
−
'''Bevis''':
+
−
 
+
−
Påståendet kan bevisas genom att använda lagen om nollte potensen (baklänges) samt andra potenslagen:
+
−
 
+
−
::::<big><math> \displaystyle{1 \over a^x} \; = \; \displaystyle{a^0 \over a^x} \; = \; a^{0-x} \; = \; a^{-x} </math></big>
+
−
 
+
−
Vi får påståendet, fast baklänges.
+
−
</div> <!-- tolv4a -->
+
−
 
+
−
 
+
−
<div class="tolv"> <!-- tolv5 -->
+
−
Att potenser med negativa exponenter är en naturlig fortsättning på potenser med positiva exponenter med nollte potensen däremellan illustrerar följande exempel:
+
−
</div> <!-- tolv5 -->
+
−
 
+
−
 
+
−
<div class="exempel"> <!-- exempel4 -->
+
−
== <b><span style="color:#931136">Varför är <math> \; 5\,^0 \, = \, 1 \; </math>?</span></b> ==
+
−
<big>
+
−
 
+
−
::::<math> \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 </math>
+
−
 
+
−
::::<math> \;\; 5^3 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 </math>
+
−
 
+
−
::::<math> \;\; 5^2 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 </math>
+
−
 
+
−
::::<math> \;\; 5^1 \; = \; {\color{Red} 1} \cdot 5 </math>
+
−
 
+
−
::::<math> \;\; {\color{Red} {5^0 \; = \; 1}} </math>
+
−
 
+
−
::::<math> \;\; 5^{-1} \; = \; \displaystyle{{\color{Red} 1} \over 5} </math>
+
−
 
+
−
::::<math> \;\; 5^{-2} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5} </math>
+
−
 
+
−
::::<math> \;\; 5^{-3} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5} </math>
+
−
 
+
−
::::<math> \;\; 5^{-4} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5 \cdot 5 } </math>
+
−
 
+
−
Att <math> \; {\color{Red} 1} </math>-orna följer med hela tiden beror på att multiplikationens ''enhet'' är <math> \, {\color{Red} 1} </math>, dvs <math> \, a \cdot {\color{Red} 1} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 1} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5^0}} \, </math> då alla <math> \, 5</math>-or har försvunnit.
+
−
</big>
+
−
</div> <!-- exempel4 -->
+
−
 
+
−
 
+
−
<div class="tolv"> <!-- tolv5 -->
+
−
Jämför med:
+
−
</div> <!-- tolv5 -->
+
−
 
+
−
 
+
−
<div class="exempel"> <!-- exempel5 -->
+
−
== <b><span style="color:#931136">Varför är <math> \; 5 \cdot 0 \, = \, 0 \; </math>?</span></b> ==
+
−
<big>
+
−
 
+
−
::::<math> \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot 3 \; = \; {\color{Red} 0} + 5 + 5 + 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot 2 \; = \; {\color{Red} 0} + 5 + 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot 1 \; = \; {\color{Red} 0} + 5 </math>
+
−
 
+
−
::::<math> \;\; {\color{Red} {5 \cdot 0 \; = \; 0}} </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot (-1) \; = \; {\color{Red} 0} - 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot (-2) \; = \; {\color{Red} 0} - 5 - 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot (-3) \; = \; {\color{Red} 0} - 5 - 5 - 5 </math>
+
−
 
+
−
::::<math> \;\; 5 \cdot (-4) \; = \; {\color{Red} 0} - 5 - 5 - 5 - 5 </math>
+
−
 
+
−
Att <math> \; {\color{Red} 0} </math>-orna följer med hela tiden beror på att additionens ''enhet'' är <math> \, {\color{Red} 0} </math>, dvs <math> \, a + {\color{Red} 0} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 0} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5 \cdot 0}} \, </math> då alla <math> \, 5</math>-or har försvunnit.
+
−
</big>
+
−
</div> <!-- exempel5 -->
+
  
 +
<br>
  
−
== <b><span style="color:#931136">Internetlänkar</span></b> ==
 
  
−
https://www.youtube.com/watch?v=BMEOkzq3Xo4
 
  
−
http://www.youtube.com/watch?v=iYgG4LUqXks
 
  
−
http://www.webbmatte.se/gym/arabiska/2/2_8_4sv.html
+
== <b><span style="color:#931136">Potensekvationer</span></b> ==
  
−
http://www.webbmatte.se/gym/arabiska/2/2_8_3sv.html
+
<br>
  
  

Versionen från 22 maj 2016 kl. 10.23

       Genomgång          Potensekvationer          Quiz          Övningar          Lathund      


Varför ekvationer? \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Exempel på en ekvation

Uppgift:

Kalle köper en flaska dryck som kostar \( \, 18 \, \) kr med pant.
Drycken (innehållet) kostar \( \, 14 \, \) kr mer än panten (flaskan).
Hur mycket kostar flaskan?
Försök att lösa uppgiften utan ekvation. Lös sedan med ekvation.

Lösning med ekvation: \( \quad\;\; x \; = \; {\rm flaskans\;pris} \)

\[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad & \\ 2\,x \, & = & 4 & \qquad & \\ x \, & = & 2 & & \end{array}\]


Svar:     Flaskan kostar \( \, 2 \; {\rm kr\,.} \quad \) Utan ekvation svarar de flesta fel (4 kr).


Läs hur man ställer upp ekvationen.


Läs längre fram en mer utförlig lösning.


\( \qquad\qquad \) \( \qquad \)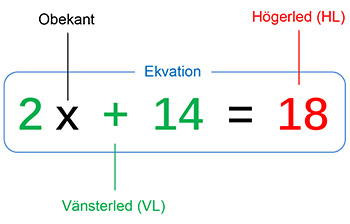Ekvation Obekant VL HL 350.jpg


Ekvation \( \; = \; \) En likhet mellan två uttryck.

Innehåller alltid ett likhetstecken och

endast en obekant. \( \qquad\;\, \) Ex. ovan:

Ekvationens lösning: \( \quad\; \)
\( x \; = \; {\color{Red} 2} \)

Kontroll:     Sätt in lösningen i ekvationen.

  VL \( \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 \)

  HL \( \, = \, 18 \)

  VL \( \; = \; \) HL \( \qquad \Longrightarrow \qquad \) OK

Kontroll kallas ibland för prövning.


Obekanta är variabler som förekommer i ekvationer. Ofta används bokstaven \( \, x \, \) för obekanta. Men det är inget måste.

Variabler är bokstäver eller platshållare för tal. De namnges med bokstäver, som lådor med etiketter. Innehållet är tal och kallas för variabelns värde.

Uttryck är en kombination av variabler, tal, räkneoperationer och parenteser som till slut, när uttrycket beräknas, ger ett värde. Inte alla ingredienser behöver ingå i ett uttryck. Ämnet har behandlats i avsnitt 3.1 Uttryck.

Formel är en likhet mellan två uttryck med minst två variabler och kommer att behandlas i avsnitt 3.5 Formler.


Ekvationslösning med inspektionsmetoden


Exemplet ovan:

  \( 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x \)

\(\quad\)
\( \, + \;\, 14 \; = \; 18 \)

  \( \;\, 4 \;\;\; + \; 14 \; = \; 18 \)

  \( \;\, \Downarrow \)

  \( \, {\color{Red} {2 \, \cdot \; x}} \;\; = \;\, 4 \qquad\quad {\color{Red} {{\rm Täck\;över\;} x}}\)

  \( \, 2 \, \cdot \; \)
\( \quad \)
\( \; = \;\, 4 \)

  \( \, 2 \, \cdot \; 2 \;\; = \;\; 4 \)

  \( \quad\;\;\; \Downarrow \)

 
\( \; {\color{Red} x} \; = \; 2 \)


Ekvationslösning med allmän metod


Exemplet ovan:

\[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad | & {\color{Red} {- \, 14}} \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ 2\,x \, & = & 4 & \qquad | & {\color{Red} {/ \; 2}} \\ \displaystyle \frac{2\,x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x \, & = & 2 & & \end{array}\]

Skrivsättet \( \quad | \quad {\color{Red} {- \, 14}} \quad\!\) är en kortform på:

Subtrahera \( \, 14 \, \) från ekvationens båda led.

Skrivsättet \( \quad | \quad {\color{Red} {/ \; 2}} \quad\;\; \) är en kortform på:

Dividera ekvationens båda led med \( \, 2 \).


God redovisningsstil:
  •    Skriv likhetstecknen exakt under varandra (samma kolumn).
  •    Kommentera, där det behövs, det du gör antingen genom att
   använda skrivsättet i exemplet ovan eller på ditt eget sätt, så
   att det blir förståeligt vad du gör.
  •    Skriv kommentarerna skilda från ekvationens lösningsgång.


Målet: \( \qquad\quad \) Att isolera \( \, {\color{Red} x} \, \) på ett led.


Metoden:


Steg 1:

  Förenkla uttrycken i ekvationens båda led så långt som

  möjligt: Se de två första raderna i exemplet ovan.


Steg 2:

  Utför samma operation på ekvationens båda led med må-

  let att isolera \( \, x \): Se raderna 3 och 5 i exemplet.

  OBS!  Förenkla under resans gång de nyuppkomna ut-

 trycken i ekvationens båda led så långt som möjligt.


Regel:    Vilken operation?    Den som isolerar \( \, x \, \).

  Rad 3 i exemplet ovan:

\[ 2\,x \, + \, 14 \; = \; 18 \qquad\quad | \;\; {\color{Red} {- \, 14}} \]

 \( \, {\color{Red} {- \, 14}} \, \) är den inversa (motsatta) operationen till \( \, + \, 14 \, \).

  Rad 5 i exemplet ovan:

\[ \;\; 2 \cdot x \; = \; 4 \qquad\quad\;\; | \;\; {\color{Red} {/ \; 2}} \]

  Eller: \( \qquad\quad\; x \cdot 2 \; = \; 4 \qquad\quad\;\;\, | \;\; {\color{Red} {/ \; 2}} \)

  \( \, {\color{Red} {/ \; 2}} \, \) är den inversa operationen till \( \, \cdot \; 2 \, \).



Ekvationer med obekanten \( \, x \, \) i båda leden




Potensekvationer






Copyright © 2010-2016 Math Online Sweden AB. All Rights Reserved.

Hämtad från "https://matte1b.mathonline.se/index.php?title=3.3_Ekvationer_2_kolumner&oldid=30018"