Skillnad mellan versioner av "1.3 Tal i decimalform"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 87: | Rad 87: | ||
<br> | <br> | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
| − | + | <b><span style="color:red">Värdesiffror</span></b> är de siffror i ett tal som är exakta | |
| − | <b><span style="color:red">Värdesiffror</span></b> är de siffror i ett tal som | + | |
| − | + | eller korrekt avrundade, exklusive inledande nollor. | |
| − | + | Avslutande nollor är värdesiffror endast om de är resultat | |
| − | + | av korrekt avrundning. | |
| − | + | Exempel: | |
| − | + | ||
| − | Exempel: | + | |
{|class="wikitable" | {|class="wikitable" | ||
! Tal !! Antal värdesiffror | ! Tal !! Antal värdesiffror | ||
Versionen från 28 juli 2017 kl. 14.19
| Genomgång Decimaltal | Avrundning & värdesiffror | Quiz | Övningar | Lathund |
| << Förra avsnitt | Nästa avsnitt >> |
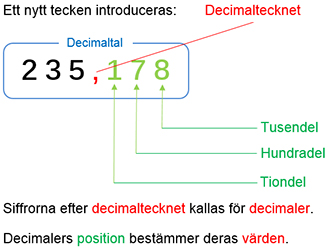
Decimaltal
Tiondelssiffran \( \quad\, {\color{LimeGreen} 1} \, \) har värdet \( \, {\color{Red}{0,1}} \, \).
Hundradelssiffran \( {\color{LimeGreen} 7} \, \) har värdet \( \, {\color{Red}{0,07}} \, \).
Tusendelssiffran \( \;\, {\color{LimeGreen} 8} \, \) har värdet \( \, {\color{Red}{0,008}} \, \).
\( 235 \, + \, {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} = \boxed{235\,{\bf{\color{Red},}}\,{\color{LimeGreen} {178}}} \)
Exempel på viktiga decimaltal
|
\( \displaystyle{ 0,5 \, = \, {1 \over 2} } \) \( \displaystyle{ 0,25 \, = \, {1 \over 4} } \) \( \displaystyle{ 0,75 \, = \, {3 \over 4} } \) |
\( \qquad\qquad \) |
\( \displaystyle{ 0,1 \, = \, {1 \over 10} } \) \( \displaystyle{ 0,01 \, = \, {1 \over 100} } \) \( \displaystyle{ 0,001 \, = \, {1 \over 1000} } \) |
\( \qquad\quad \displaystyle{ 0,333\,333\,\ldots \, = \, {1 \over 3} } \)
\( \qquad\quad \displaystyle{ 0,666\,666\,\ldots \, = \, {2 \over 3} } \)
Avrundningsregeln
Om siffran efter avrundningssiffran är:
\( \quad\; 0, \, 1, \, 2, \, 3 \; {\rm eller} \; 4 , \quad \) avrunda nedåt.
\( \quad\; 5, \, 6, \, 7, \, 8 \; {\rm eller} \; 9 , \quad \) avrunda uppåt.
Avrundningssiffran är den siffra efter vilken
alla decimaler ska kapas av.
Värdesiffror
Värdesiffror är de siffror i ett tal som är exakta
eller korrekt avrundade, exklusive inledande nollor.
Avslutande nollor är värdesiffror endast om de är resultat
av korrekt avrundning.
Exempel:
| Tal | Antal värdesiffror |
|---|---|
| a) \( \, 3,14 \, \) | Tre |
| b) \( \, 0,05 \, \) | En |
| c) \( \, 0,072 \, \) | Två |
| d) \( \, 0,40300 \, \) | Fem |
| e) \( \, 1,006 \, \) | Fyra |
Från decimaltal till bråk
Skriv \( \; 0,75 \; \) i bråkform.
\( 0,75 \, = \, \displaystyle {75 \over 100} \, = \, {15 \cdot \cancel{\color{Red} 5} \over 20 \cdot \cancel{\color{Red} 5}} \, = \, {15 \over 20} \, = \)
\( \qquad\; = \; \displaystyle {3 \cdot \cancel{\color{Red} 5} \over 4 \cdot \cancel{\color{Red} 5}} \; = \; {3 \over 4} \)
Metoden:
1. Skriv som bråk med \( 10\)-potens i nämnaren.
2. Förkorta bråket så långt som möjligt.
Från bråk till decimaltal
Skriv \( \; \displaystyle{3 \over 4} \; \) som decimaltal.
\( \displaystyle {3 \over 4} \; = \; {3 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \; = \; {15 \over 20} \; = \; {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \; = \)
\( \quad\; = \; \displaystyle {75 \over 100} \; = \; 0,75 \)
Metoden:
1. Förläng bråket tills nämnaren blir en \( 10\)-
potens.
2. Skriv resultatet från 1 till decimaltal.
Periodisk decimalutveckling
Skriv \( \; 0,333\,333\,\ldots \; \) i bråkform.
Lösning:
\( 10 \; \cdot \; 0,333\,333\,\ldots \; = \; 3,333\,333\,\ldots \quad {\rm (I)} \)
\( \underline{\;1 \;\, \cdot \; 0,333\,333\,\ldots \; = \; 0,333\,333\,\ldots} \quad {\rm (II)} \)
Vi bildar \( \; {\rm (I)-(II)} \):
\( (10-1) \cdot 0,333\,\ldots = \; 3 \)
\( \quad\;\;\; 9 \quad\, \cdot \, 0,333\ldots = \; 3 \)
\( \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{3 \over 9} \; = \; {1 \cdot \cancel{\color{Red} 3} \over 3 \cdot \cancel{\color{Red} 3}} \)
\( \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{1 \over 3} \)
\( a \cdot 10\,^n \; \) kallas grundpotensform
om \( n \, \) är heltal och \( \; 1 \leq \) \( a \) \( < 10 \; \).
Dvs \( \, a \, \) mellan \( \, 1,\ldots \, \) och \( \, 9,\ldots \; \).
Copyright © 2010-2017 Math Online Sweden AB. All Rights Reserved.