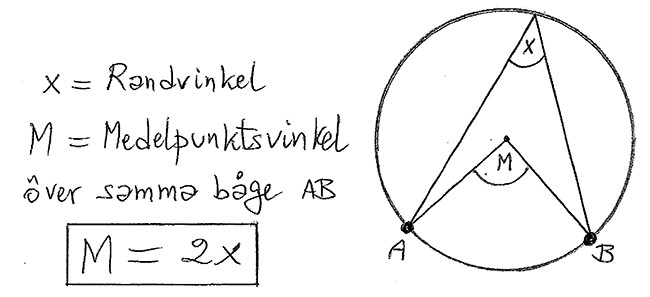Skillnad mellan versioner av "5.6 Implikation och ekvivalens"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 11: | Rad 11: | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
<big><b><span style="color:#931136"> | <big><b><span style="color:#931136"> | ||
| − | Implikation och ekvivalens är: | + | Implikation och ekvivalens</span> är: |
* Logiska verktyg i matematisk bevisföring, | * Logiska verktyg i matematisk bevisföring, | ||
Versionen från 20 februari 2020 kl. 15.18
| <<< Förra avsnitt | Genomgång | Övningar |
Implikation och ekvivalens är:
- Logiska verktyg i matematisk bevisföring,
- Logiska operatorer som kan skrivas mellan två utsagor.
En utsaga är ett påstående eller en sats som kan vara sant eller falskt.
Implikation skrivs med symbolen : \( \qquad \implies \; \). </span>
Implikation
Ekvivalens
Randvinkelsatsen
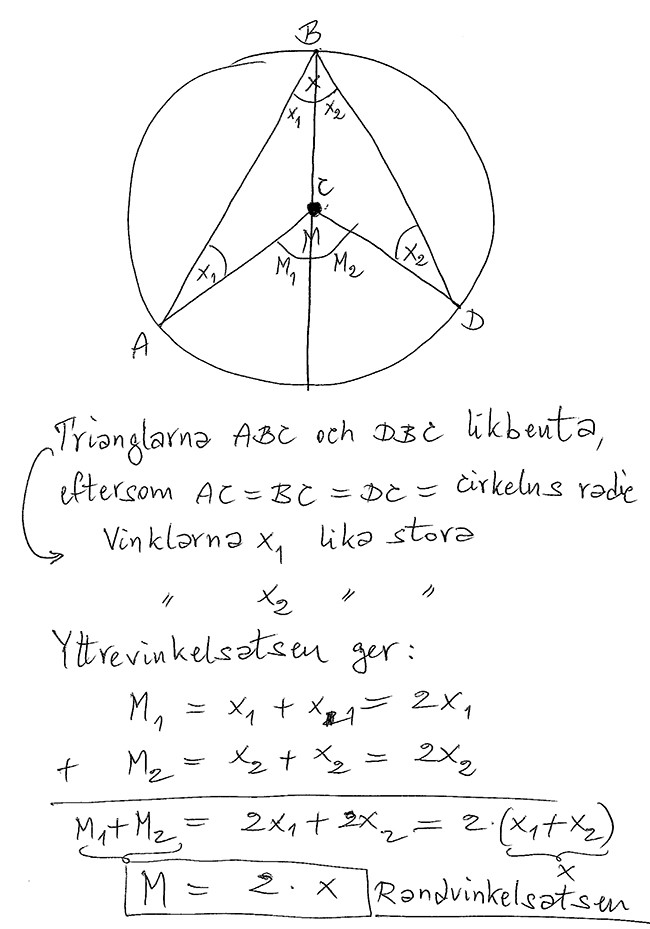
Beviset för randvinkelsatsen
Randvinkelsatsens bevis bygger i sin tur på:
- Yttervinkelsatsen.
- Satsen om att likbenta trianglars basvinklar är lika stora.
- Algebra: \( \quad a = c \quad \text{och} \quad b = d \; \implies \; a+b = c+d \)
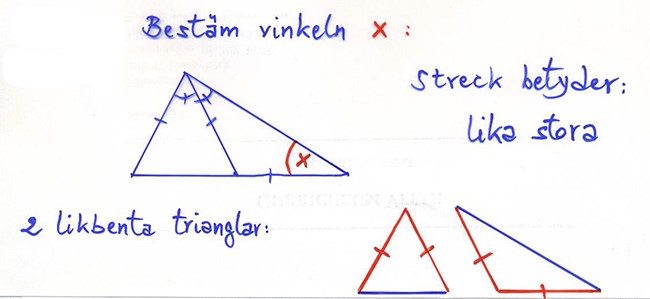
Veckans kluring (A-uppgift)
Copyright © 2020 TechPages AB. All Rights Reserved.