Versionen från 29 mars 2020 kl. 22.19

Innehåll Matte 1b

Innehåll kap 6 Sannolikhet och statistik

Genomgång

Övningar

Nästa avsnitt >>

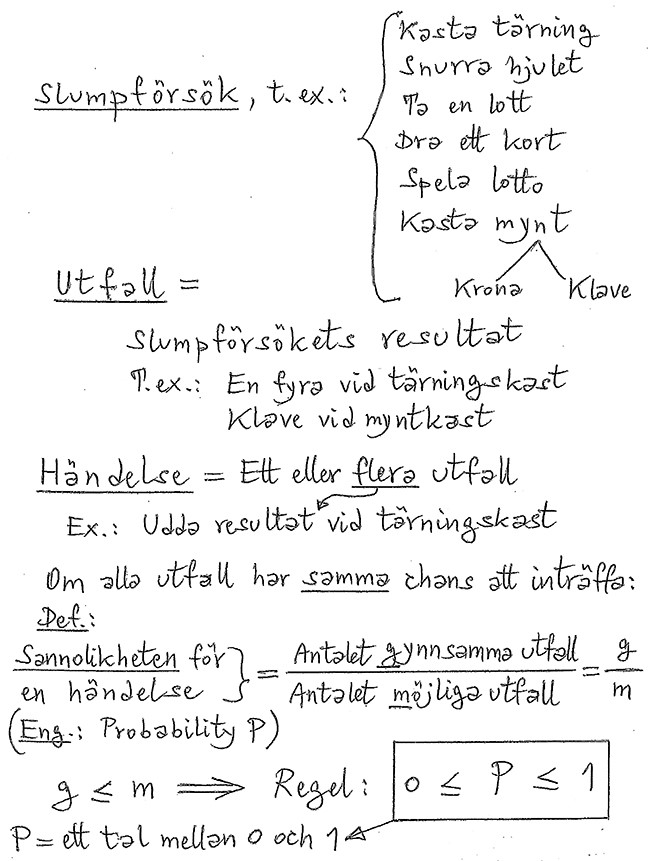
Några begrepp

Två sorters kulor i en skål

Tre sorters kulor i en skål

Addititonsregeln

Är \( \, A \, \) och \( \, B \, \) två händelser som är oberoende av varandra och är

\( \; P(A) \, \) sannolikheten för händelsen \( \, A \, \) och \( \, P(B) \, \) sannolikheten för händelsen \( \, B \, \)

så gäller: \( \qquad\qquad\quad \)

\( P(A \; \color{Red}{\text{eller}} \; B) \, = \, P(A) \; \color{Red} {\textbf{+}} \; P(B)\)

Ex. ovan Två sorters kulor i en skål med 6 gula och 2 blå kulor:

\( P(\text{gul} \; \color{Red}{\text{eller}} \; \text{blå}) \, = \, P(\text{gul}) \; \color{Red} {\textbf{+}} \; P(\text{blå}) \, = \, \displaystyle \frac{6}{9} + \frac{2}{9} = \frac{8}{9} \)

Dagens inlämningsuppgift

Lös uppgifterna 7104-7106 i 1b-boken, sid 234 (1c-boken sid 218, 6104-6106).

Skriv dina lösningar i ren form. OBS! ingen kladd.

Lösningarna ska vara tydliga, läsliga och strukturerade på ett A4-blad.

Att endast ange svaret godtas ej. Du ska redovisa hur du kommer dit.

Fota A4-bladet med din mobil och ladda upp det till Schoolitys Uppgifter.

Deadline för inlämning: kl 18 lektionsdagen.

Dagens övningar

Gör övningarna i boken Origo 1b:

Sidorna 234-235.

I Origo 1c: Sidorna 218-219.

Kolla dina resultat i bokens facit.

@@ Rad 42: / Rad 42: @@
 <math> \; P(A) \, </math> sannolikheten för händelsen <math> \, A \, </math> och <math> \, P(B) \, </math> sannolikheten för händelsen <math> \, B \, </math>
-&nbsp; så gäller: &nbsp; <math> \qquad\qquad\qquad </math> <div class="smallBoxVariant"><math> P(A \; \color{Red}{\text{eller}} \; B) \, = \, P(A) \; \color{Red} {\textbf{+}} \; P(B)</math></div>
+&nbsp; så gäller: &nbsp; <math> \qquad\qquad\quad </math> <div class="smallBoxVariant"><math> P(A \; \color{Red}{\text{eller}} \; B) \, = \, P(A) \; \color{Red} {\textbf{+}} \; P(B)</math></div>
 &nbsp; Ex. ovan <b><span style="color:#931136">Två sorters kulor i en skål</span></b> med 6 gula och 2 blå kulor:

Skillnad mellan versioner av "6.1 Sannolikhet för en händelse"