Skillnad mellan versioner av "3.7 Formler"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 16: | Rad 16: | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
<big><b> | <big><b> | ||
| + | * En <span style="color:red">ekvation</span> är en likhet mellan två [[3.1_Algebraiska_uttryck|<span style="color:blue">uttryck</span>]] som har en obekant. | ||
| − | * En formel är ett samband mellan [[3.1_Algebraiska_uttryck|<span style="color:blue">uttryck</span>]] som kan ha flera variabler. | + | * En <span style="color:red">formel</span> är ett samband mellan [[3.1_Algebraiska_uttryck|<span style="color:blue">uttryck</span>]] som kan ha flera variabler. |
* Det som skiljer en formel från en ekvation är vad man <span style="color:red">gör</span> med den: | * Det som skiljer en formel från en ekvation är vad man <span style="color:red">gör</span> med den: | ||
Versionen från 20 januari 2022 kl. 14.29
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Vad är en formel?
- En ekvation är en likhet mellan två uttryck som har en obekant.
- En formel är ett samband mellan uttryck som kan ha flera variabler.
- Det som skiljer en formel från en ekvation är vad man gör med den:
- En ekvation löser man, medan med en formel beräknar man något.
- För att beräkna det man vill, måste man ofta skriva om formeln.
- Man säger då: man löser ut en variabel ur formeln.
Att ställa upp formler
Exempel 1 Sparkapital
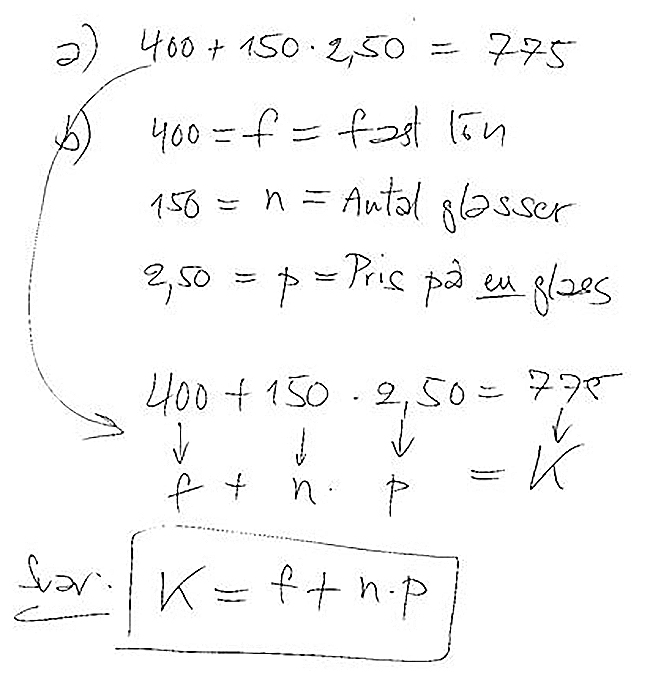
Exempel 2 Glassförsäljning
Omskrivning av formler
Copyright © 2022 TechPages AB. All Rights Reserved.