Versionen från 4 maj 2022 kl. 07.44

Genomgång

Övningar

Flera föremål

Titta på detta videoklipp (4:13 min).

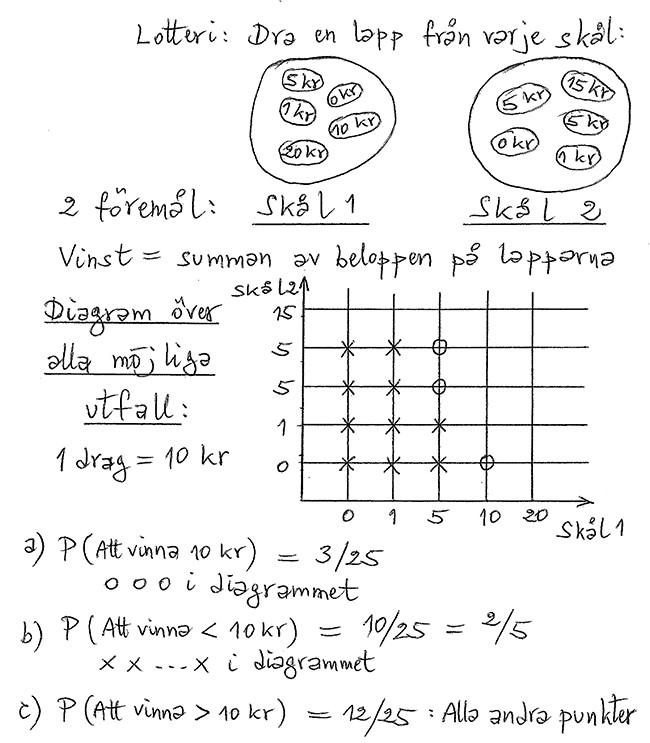
Rita ett diagram över alla möjliga utfall, även kallat utfallsrummet.

Se exempel i videoklippet ovan. Generellt lyder regeln:

\( \qquad\qquad\qquad\quad \)

Kartlägg utfallsrummet.

Ett sätt att kartlägga utfallsrummet är att rita ett diagram över alla möjliga utfall.

Två föremål ger ett 2D diagram liknande ett koordinatsystem.

Tre föremål skulle ge ett 3D diagram liknande en kub: svårt att rita.

Flera föremål ger ett flerdimensionellt utfallsrum: omöjligt att rita!

Ytterligare exempel på slumpförsök med två föremål:

Lös uppgifterna 7110-7113 i 1b-boken, sid 235 (1c-boken sid 219, 6110-6113).

Skriv ren dina lösningar tydliga, läsliga och strukturerade på ett A4-blad.

Motivera dina svar.

Fota A4-bladet med din mobil och ladda upp det till Schoolitys Uppgifter.

Deadline för inlämning: kl 18 lektionsdagen. Maila inte dina lösningar.

Gör övningarna i boken Origo 1b:

Sid 235, uppg. 7110-7119.

I Origo 1c: Sid 219, uppg. 6110-6119.

Kolla dina resultat i bokens facit.

@@ Rad 6: / Rad 6: @@
 {{Selected tab|[[6.3 Slumpförsök med flera föremål|Genomgång]]}}
 {{Not selected tab|[[6.3 Övningar till Slumpförsök med flera föremål|Övningar]]}}
-{{Not selected tab|[[6.4 Experimentella sannolikheter|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
+<!-- {{Not selected tab|[[6.4 Experimentella sannolikheter|Nästa avsnitt&nbsp;&nbsp;>> ]]}} -->
+{{Not selected tab|[[6.5 Slumpförsök i flera steg|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 | style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 |}