1.3 Tal i decimalform

Genomgång

Quiz

Övningar

Genomgång+

Avrundning & värdesiffror

<<  Förra avsnitt

Nästa avsnitt  >>

Tal i decimalform   =   Decimaltal   =   Tal mellan två heltal

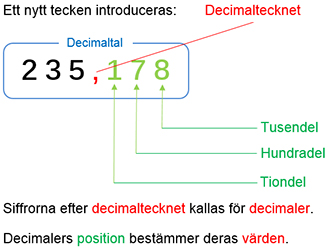
Fortsättning på det decimala positionssystemet:

Tiondelssiffran \( \quad\, {\color{LimeGreen} 1} \, \) har värdet \( \, {\color{Red}{0,1}} \, \).

Hundradelssiffran \( {\color{LimeGreen} 7} \, \) har värdet \( \, {\color{Red}{0,07}} \, \).

Tusendelssiffran \( \;\, {\color{LimeGreen} 8} \, \) har värdet \( \, {\color{Red}{0,008}} \, \).

\( 235 \, + \, {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} = \boxed{235\,{\bf{\color{Red},}}\,{\color{LimeGreen} {178}}} \)

Heltal i decimalform

Ex

\( 7\,142 \; = \; 7\,142 \, {\bf{\color{Red},}} \, {\color{LimeGreen} {000\, \ldots}} \)

Generellt

Alla heltal kan skrivas i decimalform med deci-

maltecknet och nollor som decimaler. Slut-

sats: Alla heltal är decimaltal, men inte tvärtom.

Exempel på viktiga decimaltal

\( \displaystyle{ 0,5 \, = \, {1 \over 2} } \) \( \displaystyle{ 0,25 \, = \, {1 \over 4} } \) \( \displaystyle{ 0,75 \, = \, {3 \over 4} } \)

\( \qquad\qquad \)

\( \displaystyle{ 0,1 \, = \, {1 \over 10} } \) \( \displaystyle{ 0,01 \, = \, {1 \over 100} } \) \( \displaystyle{ 0,001 \, = \, {1 \over 1000} } \)

\( \qquad\quad \displaystyle{ 0,333\,333\,\ldots \, = \, {1 \over 3} } \)

\( \qquad\quad \displaystyle{ 0,666\,666\,\ldots \, = \, {2 \over 3} } \)

Placering av decimaltal på tallinjen

Kunskapen om decimaltalens värde ska hjälpa oss att ha en uppfattning om decimaltalens storlek och deras korrekta placering på tallinjen.

Ex.

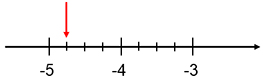
Vilket decimaltal pekar pilen på?

Lösning:

Vi befinner oss på den negativa delen av tallinjen:

• Skalans minsta steg på tallinjen är: \( \; 1 \,/\, 4 \, = \, \displaystyle {1 \over 4} \, = \, 0,25 \)
• \( \; 1 \,/\, 4 \, = \, \displaystyle{{1 \over 4} \, = \, {1 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \, = \, {5 \over 20} \, = \, {5 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \, = \, {25 \over 100}} \, = \, 0,25 \)
• Det sökta decimaltalet ligger mellan heltalen \( \, -4 \, \) och \( \, -5 \).
• Utgående från \( \, -4 \, \) rör vi oss tre steg till vänster för att hitta det sökta decimaltalet: \( \, -4 \,-\, 0,25 \,-\, 0,25 \,-\, 0,25 \, = \, {\color{Red} {-4,75}}\).

Omvandlingen av \( \, 1 \,/\, 4 \, \) till \( \, 0,25 \, \) i förklaringen ovan är ett exempel på användningen av viktiga decimaltal. Här sammanfattas några:

Avrundningsregeln

Om siffran efter avrundningssiffran är:

\( \quad\; 0, \, 1, \, 2, \, 3 \; {\rm eller} \; 4 , \quad \) avrunda nedåt.

\( \quad\; 5, \, 6, \, 7, \, 8 \; {\rm eller} \; 9 , \quad \) avrunda uppåt.

Avrundningssiffran är den siffra efter vilken

alla decimaler ska kapas av.

Värdesiffror

Tal	Antal värdesiffror
\( \qquad 3,14 \quad \)	Tre
\( \qquad 0,05 \quad \)	En
\( \qquad 0,072 \quad \)	Två
\( \qquad 0,40300 \quad \)	Fem
\( \qquad 1,006 \, \)	Fyra

Från decimaltal till bråk

Skriv \( \; 0,75 \; \) i bråkform.

Lösning:

\( 0,75 \, = \, \displaystyle {75 \over 100} \, = \, {15 \cdot \cancel{\color{Red} 5} \over 20 \cdot \cancel{\color{Red} 5}} \, = \, {15 \over 20} \, = \)

\( \qquad\; = \; \displaystyle {3 \cdot \cancel{\color{Red} 5} \over 4 \cdot \cancel{\color{Red} 5}} \; = \; {3 \over 4} \)

Metoden:

1.   Skriv som bråk med \( 10\)-potens i nämnaren.

2.   Förkorta bråket så långt som möjligt.

Från bråk till decimaltal

Skriv \( \; \displaystyle{3 \over 4} \; \) som decimaltal.

Lösning:

\( \displaystyle {3 \over 4} \; = \; {3 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \; = \; {15 \over 20} \; = \; {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \; = \displaystyle {75 \over 100} \; = \)

\( \quad\; = \; 0,75 \)

Metoden:

1.   Förläng bråket tills nämnaren blir en \( 10\)-

      potens.

2.   Skriv resultatet från 1 till decimaltal.

Periodisk decimalutveckling

Skriv \( \; 0,333\,333\,\ldots \; \) i bråkform.

Lösning:

\( 10 \; \cdot \; 0,333\,333\,\ldots \; = \; 3,333\,333\,\ldots \quad {\rm (I)} \)

\( \underline{\;1 \;\, \cdot \; 0,333\,333\,\ldots \; = \; 0,333\,333\,\ldots} \quad {\rm (II)} \)

Vi bildar \( \; {\rm (I)-(II)} \):

\( (10-1) \cdot 0,333\,\ldots = \; 3 \)

\( \quad\;\;\; 9 \quad\, \cdot \, 0,333\ldots = \; 3 \)

\( \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{3 \over 9} \; = \; {1 \cdot \cancel{\color{Red} 3} \over 3 \cdot \cancel{\color{Red} 3}} \)

\( \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{1 \over 3} \)

Tal	Perioden	Skrivsätt
\( \;\; 0,333\,333\,\ldots \)	3	\( 0,\bar{3} \)
\( \;\; 0,666\,666\,\ldots \)	6	\( 0,\bar{6} \)
\( \;\; 0,18181818\,\ldots \)	18	\( 0,\overline{18} \)
\( \;\; 1,16666666\,\ldots \)	6	\( 1,1\bar{6} \)
\( \;\; 0,09090909\,\ldots \)	09	\( 0,\overline{09} \)
\( \;\; 0,045454545\,\ldots \)	45	\( 0,0\overline{45} \)

Copyright © 2023 TechPages AB. All Rights Reserved.