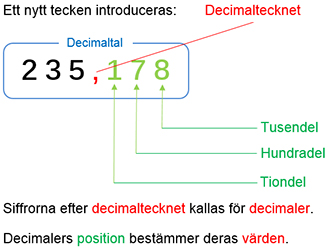
1.3 Tal i decimalform

Genomgång Decimaltal

Avrundning & värdesiffror

Quiz

Övningar

Lathund

<<  Förra avsnitt

Nästa avsnitt  >>

Decimaltal

Tiondelssiffran \( \quad\, {\color{LimeGreen} 1} \, \) har värdet \( \, {\color{Red}{0,1}} \, \).

Hundradelssiffran \( {\color{LimeGreen} 7} \, \) har värdet \( \, {\color{Red}{0,07}} \, \).

Tusendelssiffran \( \;\, {\color{LimeGreen} 8} \, \) har värdet \( \, {\color{Red}{0,008}} \, \).

\( 235 \, + \, {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} = \boxed{235\,{\bf{\color{Red},}}\,{\color{LimeGreen} {178}}} \)

Exempel på viktiga decimaltal

\( \displaystyle{ 0,5 \, = \, {1 \over 2} } \) \( \displaystyle{ 0,25 \, = \, {1 \over 4} } \) \( \displaystyle{ 0,75 \, = \, {3 \over 4} } \)

\( \qquad\quad \)

\( \displaystyle{ 0,1 \, = \, {1 \over 10} } \) \( \displaystyle{ 0,01 \, = \, {1 \over 100} } \) \( \displaystyle{ 0,001 \, = \, {1 \over 1000} } \)

\( \qquad\quad \displaystyle{ 0,333\,333\,\ldots \, = \, {1 \over 3} } \)

\( \qquad\quad \displaystyle{ 0,666\,666\,\ldots \, = \, {2 \over 3} } \)

Från decimaltal till bråk

Skriv \( \; 0,75 \; \) i bråkform.

\( \; 0,75 \, = \, \displaystyle {75 \over 100} \, = \, {15 \cdot \cancel{\color{Red} 5} \over 20 \cdot \cancel{\color{Red} 5}} \, = \, {15 \over 20} \, = \, \)

\( \qquad\;\; = \, \displaystyle {3 \cdot \cancel{\color{Red} 5} \over 4 \cdot \cancel{\color{Red} 5}} \, = \, = \, {3 \over 4} \)

Metoden: 1.   Skriv som bråk med 10-potens i nämnaren.

2.   Förkorta bråket så långt som möjligt.

Från bråk till decimaltal

\( \, y \, = \, \lg\,x \, \) är den inversa (motsatta)

funktionen till \( \, y \, = \, 10\,^x \, \), dvs:

\( \lg\,(10^{\,{\color{Red} x}}) = {\color{Red} x} \quad {\rm och\; } \quad 10^{\,\lg{\color{Red} x}} = {\color{Red} x} \)

\( \boxed{\text{LOG}} \, \) och \( \, 10 \) \( \boxed{\text{ ^ }} \, \) tar ut varandra.

Exempel:

\( \boxed{\text{LOG}}\) \(({\color{Red} {1,5}}) \quad = \quad \cdots\cdots \)

\( 10 \) \( \boxed{\text{ ^ }} \; \boxed{\text{ANS}}\) \( \;\;\; = \quad\;\, {\color{Red} {1,5}} \)

\( \;\; \boxed{\text{ANS}} \) är räknarens sist visade svar.

\( 10 \) \( \boxed{\text{ ^ }}\) \({\color{Red} {2,5}} \quad\;\;\, = \quad \) \( \cdots\cdots \)

\( \boxed{\text{LOG}} \, \left(\,\boxed{\text{ANS}}\,\right)\) \( = \quad\;\, {\color{Red} {2,5}} \)

Exponentialekvationer av typ \( \; 10\,^x \, = \, b \)

\(\begin{array}{rcll} 10^{\,x} & = & 68 & | \; \lg\,(\,\cdot\,) \\ {\color{Red} {\lg}}\,({\color{Red} {10}}^{\,x}) & = & \lg\,68 & \\ x & = & \lg\,68 & \\ x & = & 1,8325089\ldots & \\ \end{array}\)

Kontroll: \( \qquad 10^{\,1,832508913} \, = \, 68 \)

I rad 1 logaritmeras ekvationens båda led.

I rad 2➛3 ger inversegenskapen: \( {\color{Red} {\lg}}({\color{Red} {10}}^{\,x}) = x \)

Generellt:

Exponentialekvationen \( \;\;\; 10\,^x \, = \, b \)

har lösningen: \( \qquad\qquad\quad x \, = \, \lg\,b \)

Copyright © 2010-2017 Math Online Sweden AB. All Rights Reserved.