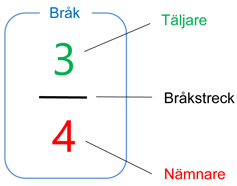
1.5 Tal i bråkform

Genomgång

\( \qquad\quad \)

Bråkstrecket betyder division:

\( \quad\; \displaystyle \frac{{\color{Limegreen} 3}}{{\color{Red} 4}} \; = \; {\color{Limegreen} 3} \, / \, {\color{Red} 4} \; = \; 0,75 \)

Förkortning av bråk

Förkorta bråken så långt som möjligt:

\( \quad \displaystyle \frac{2}{4} \; = \; \frac{1 \cdot 2}{2 \cdot 2} \; = \; \frac{1 \cdot \cancel{\color{Red} 2}}{2 \cdot \cancel{\color{Red} 2}} \; = \; \frac{1}{2} \)

\( \quad \displaystyle \frac{6}{9} \; = \; \frac{2 \cdot 3}{3 \cdot 3} \; = \; \frac{2 \cdot \cancel{\color{Red} 3}}{3 \cdot \cancel{\color{Red} 3}} \; = \; \frac{2}{3} \)

\( \quad \displaystyle \frac{10}{15} \; = \; \frac{2 \cdot 5}{3 \cdot 5} \; = \; \; \frac{2 \cdot \cancel{\color{Red} 5}}{3 \cdot \cancel{\color{Red} 5}} \; = \; \frac{2}{3} \)

\( \quad \displaystyle \frac{8}{24} \; = \; \frac{\cancel{\color{Red} 2} \cdot 4}{\cancel{\color{Red} 2} \cdot 12} \, = \, \frac{\cancel{\color{Red} 2} \cdot 2}{\cancel{\color{Red} 2} \cdot 6} \, = \, \frac{\cancel{\color{Red} 2} \cdot 1}{\cancel{\color{Red} 2} \cdot 3} \, = \, \frac{1}{3} \)

Metoden:

Hitta en gemensam faktor hos täljaren och nämna-

ren. Dividera både täljaren och nämnaren med

samma gemensamma faktor.

Förkortning och förlängning

Förlängning av bråk

Förläng bråken:

1) \( \;\; \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 3}}{4 \cdot {\color{Red} 3}} \; = \; \frac{9}{12} \)

2) \( \;\; \displaystyle \frac{2}{3} \; = \; \frac{2 \cdot {\color{Red} 4}}{3 \cdot {\color{Red} 4}} \; = \; \frac{8}{12} \)

3) \( \;\; \displaystyle \frac{3}{4} \; = \; \frac{3 \cdot {\color{Red} 5}}{4 \cdot {\color{Red} 5}} \; = \; \frac{15}{20} \; = \; \frac{15 \cdot {\color{Red} 5}}{20 \cdot {\color{Red} 5}} \; = \; \frac{75}{100} \)

4) \( \;\; \displaystyle {1 \over 8} \; = \; {1 \cdot {\color{Red} 5} \over 8 \cdot {\color{Red} 5}} \; = \; {5 \over 40} \; = \; {5 \cdot {\color{Red} 5} \over 40 \cdot {\color{Red} 5}} \; = \; {25 \over 200} \; = \)

\( \qquad\;\;\; \displaystyle = \; {25 \cdot {\color{Red} 5} \over 200 \cdot {\color{Red} 5}} \; = \; {125 \over 1\,000} \)

Metoden:

Multiplicera täljaren och nämnaren med samma tal.

Varför förlängning?

Exemplen 1) och 2) visar att bråken genom förläng-

ning kan få samma nämnare, vilket gör att man t.ex.

kan jämföra dem med varandra: \( \quad\;\; \displaystyle \frac{9}{12} \, > \, \frac{8}{12} \)

och därmed avgöra: \( \qquad\qquad\qquad\; \displaystyle \frac{3}{4} \, > \, \frac{2}{3} \)

Dessutom kam man addera och subtrahera dem.

Exemplen 3) och 4) visar att bråken genom förläng-

ning kan få en \( \, 10\)-potens i nämnaren, vilket t.ex.

gör att man direkt kan skriva dem till decimaltal.

Slutsats:

Både förkortning och förlängning bibehåller

bråkets värde.

Addition och subtraktion

Exempel på addition och subtraktion

Multiplikation och division