4.8 Beräkningar med funktioner
| << Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
Exempel på funktioner
\[ y \, = \, f(x) \, = \, 4\,x + 12 \]
\[ y \, = \, g(x) \, = \, 3\,x^2 + 5\,x - 16 \]
\[ y \, = \, h(x) \, = \, 8\,x^3 - 4\,x\]
En funktions värde
En funktion definieras med uttrycket till höger om likhetstecknet, kallat funktionsuttryck.
Därför är funktionens värde uttryckets värde. Precis som ett uttryck har en
funktion inget värde för sig utan får ett värde endast för ett visst \(\,\color{Red}x\,\).
Exempel: Beräkna följande funktions värde för \( \, \color{Red}{x = 0,5} \, \):
- \[ y \, = \, h(x) \, = \, 8\,x^3 - 4\,x \]
Lösning: Vi sätter in \( 0,5\,\) för \(x\,\) i funktionen och beräknar funktionsuttryckets värde:
- \[ h(0,5) \, = \, 8 \cdot 0,5^3 - 4 \cdot 0,5 = 8 \cdot 0,125 - 2 = 1 - 2 = -1 \,\]
För andra värden på \(\,x\,\) kommer funktionen att ha andra värden.
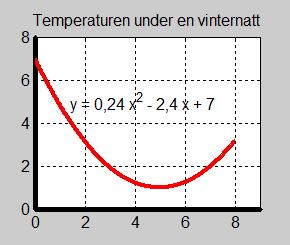
Uppgift Vinternatt
Dagens inlämningsuppgift (krävs för närvaro)
- Lös uppgiften Vinternatt.
- Skriv dina uträkningar läsliga, tydliga och strukturerade på A4 blad.
- Fota A4-bladen med din mobil.
- Ladda upp dina bilder till Schoolitys Uppgifter.
Dagens övningar
Gör övningarna i boken Origo 1b:
Sidan 180
I Origo 1c: Sidan +++
Kolla dina resultat i bokens facit.
Copyright © 2020 TechPages AB. All Rights Reserved.