1.3 Tal i decimalform
| Genomgång | Quiz | Övningar | Genomgång+ | Avrundning & värdesiffror | Nästa avsnitt >> |
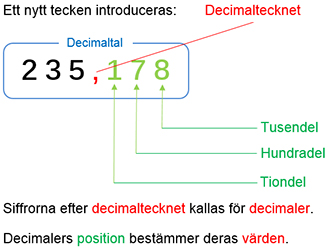
Tal i decimalform = Tal mellan två heltal
Fortsättning på det decimala positionssystemet:
Tiondelssiffran \( \quad\, {\color{LimeGreen} 1} \, \) har värdet \( \, {\color{Red}{0,1}} \, \).
Hundradelssiffran \( {\color{LimeGreen} 7} \, \) har värdet \( \, {\color{Red}{0,07}} \, \).
Tusendelssiffran \( \;\, {\color{LimeGreen} 8} \, \) har värdet \( \, {\color{Red}{0,008}} \, \).
\( 235 \, + \, {\color{Red}{0,1 \, + \, 0,07 \, + \, 0,008}} = \boxed{235\,{\bf{\color{Red},}}\,{\color{LimeGreen} {178}}} \)
Heltal i decimalform
Ex
\( 7\,142 \; = \; 7\,142 \, {\bf{\color{Red},}} \, {\color{LimeGreen} {000\, \ldots}} \)
Generellt
Alla heltal kan skrivas i decimalform med deci-
maltecknet och nollor som decimaler. Slut-
sats: Alla heltal är decimaltal, men inte tvärtom.
Exempel på viktiga decimaltal
|
\( \displaystyle{ 0,5 \, = \, {1 \over 2} } \) \( \displaystyle{ 0,25 \, = \, {1 \over 4} } \) \( \displaystyle{ 0,75 \, = \, {3 \over 4} } \) |
\( \qquad\qquad \) |
\( \displaystyle{ 0,1 \, = \, {1 \over 10} } \) \( \displaystyle{ 0,01 \, = \, {1 \over 100} } \) \( \displaystyle{ 0,001 \, = \, {1 \over 1000} } \) |
\( \qquad\quad \displaystyle{ 0,333\,333\,\ldots \, = \, {1 \over 3} } \)
\( \qquad\quad \displaystyle{ 0,666\,666\,\ldots \, = \, {2 \over 3} } \)
Placering av decimaltal på tallinjen
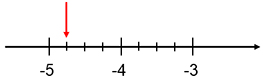
Ex.: Vilket decimaltal pekar pilen på?
Lösning:
Vi befinner oss på den negativa delen av tallinjen.
Det sökta decimaltalet ligger mellan heltalen \( \, -4 \, \) och \( \, -5 \).
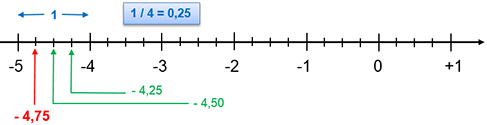
Ett streck på tallinjen: \( 1/4 = {1 \over 4} = {1 \cdot {\color{Red} {25}} \over 4 \cdot {\color{Red} {25}}} = {25 \over 100} \, = \, 0,25 \)
Starta vid \( \, -4 \, \) och gå tre steg till vänster :
\( \, -4 \,-\, 0,25 \,-\, 0,25 \,-\, 0,25 \, = \, {\color{Red} {-4,75}}\).
Avrundningsregeln
Om siffran efter avrundningssiffran är:
\( \quad\; 0, \, 1, \, 2, \, 3 \; {\rm eller} \; 4 , \quad \) avrunda nedåt.
\( \quad\; 5, \, 6, \, 7, \, 8 \; {\rm eller} \; 9 , \quad \) avrunda uppåt.
Avrundningssiffran är den siffra efter vilken
alla decimaler ska kapas av.
Värdesiffror
| Tal | Antal värdesiffror |
|---|---|
| \( \qquad 3,14 \quad \) | Tre |
| \( \qquad 0,05 \quad \) | En |
| \( \qquad 0,072 \quad \) | Två |
| \( \qquad 0,40300 \quad \) | Fem |
| \( \qquad 1,006 \, \) | Fyra |
Från decimaltal till bråk
Skriv \( \; 0,75 \; \) i bråkform.
Lösning:
\( 0,75 \, = \, \displaystyle {75 \over 100} \, = \, {15 \cdot \cancel{\color{Red} 5} \over 20 \cdot \cancel{\color{Red} 5}} \, = \, {15 \over 20} \, = \)
\( \qquad\; = \; \displaystyle {3 \cdot \cancel{\color{Red} 5} \over 4 \cdot \cancel{\color{Red} 5}} \; = \; {3 \over 4} \)
Metoden:
1. Skriv som bråk med \( 10\)-potens i nämnaren.
2. Förkorta bråket så långt som möjligt.
Från bråk till decimaltal
Skriv \( \; \displaystyle{3 \over 4} \; \) som decimaltal.
Lösning:
\( \displaystyle {3 \over 4} \; = \; {3 \cdot {\color{Red} 5} \over 4 \cdot {\color{Red} 5}} \; = \; {15 \over 20} \; = \; {15 \cdot {\color{Red} 5} \over 20 \cdot {\color{Red} 5}} \; = \displaystyle {75 \over 100} \; = \)
\( \quad\; = \; 0,75 \)
Metoden:
1. Förläng bråket tills nämnaren blir en \( 10\)-
potens.
2. Skriv resultatet från 1 till decimaltal.
Periodisk decimalutveckling
Skriv \( \; 0,333\,333\,\ldots \; \) i bråkform.
Lösning:
\( 10 \; \cdot \; 0,333\,333\,\ldots \; = \; 3,333\,333\,\ldots \quad {\rm (I)} \)
\( \underline{\;1 \;\, \cdot \; 0,333\,333\,\ldots \; = \; 0,333\,333\,\ldots} \quad {\rm (II)} \)
Vi bildar \( \; {\rm (I)-(II)} \):
\( (10-1) \cdot 0,333\,\ldots = \; 3 \)
\( \quad\;\;\; 9 \quad\, \cdot \, 0,333\ldots = \; 3 \)
\( \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{3 \over 9} \; = \; {1 \cdot \cancel{\color{Red} 3} \over 3 \cdot \cancel{\color{Red} 3}} \)
\( \qquad\; 0,333\,333\,\ldots \: = \: \displaystyle{1 \over 3} \)
| Tal | Perioden | Skrivsätt |
|---|---|---|
| \( \;\; 0,333\,333\,\ldots \) | 3 | \( 0,\bar{3} \) |
| \( \;\; 0,666\,666\,\ldots \) | 6 | \( 0,\bar{6} \) |
| \( \;\; 0,18181818\,\ldots \) | 18 | \( 0,\overline{18} \) |
| \( \;\; 1,16666666\,\ldots \) | 6 | \( 1,1\bar{6} \) |
| \( \;\; 0,09090909\,\ldots \) | 09 | \( 0,\overline{09} \) |
| \( \;\; 0,045454545\,\ldots \) | 45 | \( 0,0\overline{45} \) |
Icke-periodisk decimalutveckling
Så kallas tal som har oändligt många decimaler utan
något upprepande mönster (utan period), t.ex.:
- \[\sqrt{2} \; = \; 1,4142135623730950488016887\ldots \, \]
Detta decimaltal är en icke-periodisk decimalutveckling,
för det har oändligt många decimaler utan period, dvs
utan grupper av siffror som upprepas. Man kallar dem
för irrationella. \( \sqrt{2} \, \) är ett exempel på ett irrationellt tal.
Ändå är \( \sqrt{2} \cdot \sqrt{2} = 2 \, \) ett heltal, se Olika typer av tal.
Ett annat exempel är talet \( \, \pi \). Det finns oändligt
många irrationella tal. De kan inte skrivas i bråkform.
Det enda sättet att hantera dem är att avrunda dem.
Hur man gör det visas i Avrundning och värdesiffror.
Copyright © 2023 TechPages AB. All Rights Reserved.