3.3 Ekvationer+

Genomgång Ekvationer

Genomgång Potensekvationer

Quiz

Övningar

Lathund

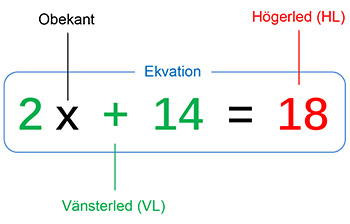
Exempel på en ekvation

\( \qquad \)

Ekvation \( \; = \; \) En likhet mellan två uttryck.

Innehåller alltid ett likhetstecken och

endast en obekant. \( \qquad\;\, \) Ex. ovan:

Ekvationens lösning: \( \quad\; \)

\( x \; = \; {\color{Red} 2} \)

Kontroll:     Sätt in lösningen i ekvationen.

  VL \( \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 \)

  HL \( \, = \, 18 \)

  VL \( \; = \; \) HL \( \qquad \Rightarrow \qquad \) OK

Kontroll kallas ibland för prövning.

Ekvationslösning med inspektionsmetoden

Exemplet ovan:

  \( 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {{\rm Täck\;över\;} x}}\)-\( {\color{Red} {\rm termen}} \)

\(\quad\)

\( \, + \;\, 14 \; = \; 18 \)

  \( \;\, 4 \;\;\; + \; 14 \; = \; 18 \)

  \( \;\, \Downarrow \)

  \( \, {\color{Red} {2 \, \cdot \; x}} \;\; = \;\, 4 \qquad\quad {\color{Red} {{\rm Täck\;över\;} x}}\)

  \( \, 2 \, \cdot \; \)

\( \quad \)

\( \; = \;\, 4 \)

  \( \, 2 \, \cdot \; 2 \;\; = \;\; 4 \)

  \( \quad\;\;\; \Downarrow \)

 

\( \; {\color{Red} x} \; = \; 2 \)

Ekvationslösning med allmän metod

Exemplet ovan:

\[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad | & {\color{Red} {- \, 14}} \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ 2\,x \, & = & 4 & \qquad | & {\color{Red} {/ \; 2}} \\ \displaystyle \frac{2\,x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x \, & = & 2 & & \end{array}\]

Skrivsättet \( \quad | \quad {\color{Red} {- \, 14}} \quad\!\) är en kortform på:

Subtrahera \( \, 14 \, \) från ekvationens båda led.

Skrivsättet \( \quad | \quad {\color{Red} {/ \; 2}} \quad\;\; \) är en kortform på:

Dividera ekvationens båda led med \( \, 2 \).

Tillvägagångssättet:

Målet: \( \qquad\quad \) Att isolera \( \, {\color{Red} x} \, \) på ett led.

Steg 1:

  Förenkla uttrycken i ekvationens båda led så långt som

  möjligt: Se de två första raderna i exemplet ovan.

Steg 2:

  Utför samma operation på ekvationens båda led med må-

  let att isolera \( \, x \, \) på ett led: Se raderna 3 och 5 i exemplet.

  OBS!  Förenkla under resans gång de nyuppkomna ut-

 trycken i ekvationens båda led så långt som möjligt.

Vilken operation?

  Rad 3 i exemplet ovan:

\[ 2\,x \, + \, 14 \; = \; 18 \qquad | {\color{Red} {- \, 14}} \]

 \( \, {\color{Red} {- \, 14}} \, \) är den inversa (motsatta) operationen till \( \, + \, 14 \, \).

  Rad 5 i exemplet ovan:

\[ \quad 2 \cdot x \; = \; 4 \qquad | {\color{Red} {/ \; 2}} \]

Eller: \( \qquad\qquad x \cdot 2 \; = \; 4 \qquad | {\color{Red} {/ \; 2}} \)

 \( \, {\color{Red} {/ \; 2}} \, \) är den inversa operationen till \( \, \cdot \; 2 \, \).

Rekommendationer:

• Skriv likhetstecknen exakt under varandra (samma kolumn).

• Kommentera ditt tillvägagångssätt, där det behövs, antingen

genom att använda det i exemplet ovan införda skrivsättet

eller på ditt eget sätt, så att det blir förståeligt vad du gör.

• Skriv kommentarerna skilda från ekvationens lösningsgång.

Copyright © 2010-2016 Math Online Sweden AB. All Rights Reserved.