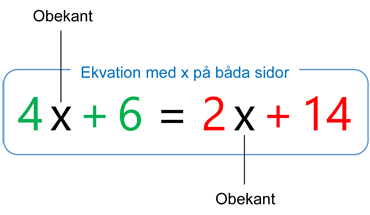
3.4 Lathund till Ekvationer med x på båda sidor
| Genomgång Ekvationer med... | Quiz | Övningar | Lathund | Nästa avsnitt >> |
| << Förra avsnitt |
Ekvation med EN obekant på båda leden
Lösning:
\(\begin{array}{rcl} 4\,x \, + \, 6 & = & 2\,x \, + \, 14 \\ \quad 4\,x \, + \, 6 \; {\color{Red} {- \; 2\,x}} & = & 2\,x \, + \, 14 \; {\color{Red} {- \; 2\,x}} \quad \\ 2\,x \, + \, 6 & = & 14 \\ 2\,x \, + \, 6 \; {\color{Red} {- \; 6}} & = & 14 \; {\color{Red} {- \; 6}} \\ 2 \cdot x \, & = & 8 \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{8}{{\color{Red} {2}}} \\ x \, & = & 4 \end{array}\)
Metoden:
Steg 1
Samla alla \( x\)-termer på det led som har den
"större" \( x\)-termen. I exemplet ovan på VL:
- \[\begin{array}{rcl} x \, + \, (x \, + \, 14) & = & 18 \\ x \, + \, x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 & = & 18 \end{array}\]
Steg 2
Utför samma operation på båda leden:
- \[\begin{array}{rcl} 2\,x \, + \, 14 & = & 18 \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} \\ 2\,x \, & = & 4 \end{array}\]
Vilken operation?
Den inversa operation som isolerar \( x\)-termen.
\( \;\;\; {\color{Red} {- \, 14}} \, \) är den inversa operationen till \( \, + \, 14 \)
Steg 3
Utför samma operation på båda leden:
- \[\begin{array}{rclcl} \quad\; 2 \cdot x \, & = & 4 & & \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x & = & 2 & & \end{array}\]
Vilken operation?
Den inversa operation som isolerar \( \, x \, \).
\( \quad\;\; {\color{Red} {/ \; 2}} \, \) är den inversa operationen till \( \, \cdot \; 2 \)
Copyright © 2010-2017 Math Online Sweden AB. All Rights Reserved.