3.4 Lathund till Ekvationer med x på båda sidor

Genomgång Ekvationer med...

Quiz

Övningar

Lathund

Nästa avsnitt >>

<< Förra avsnitt

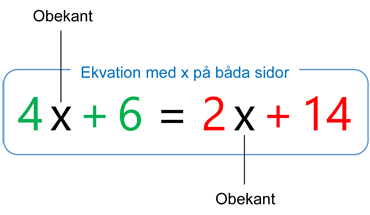
Fall 1: \( x\)-term med större koefficient på VL

\( \qquad \)

\( \qquad {\bf{\color{LimeGreen} 4}} \, \) är koefficienten till \( \, 4\,x \, \).

\( \qquad {\bf{\color{Red} 2}} \, \) är koefficienten till \( \, 2\,x \): \( \quad {\bf{\color{LimeGreen} 4}} \, > {\bf{\color{Red} 2}} \)

Steg 1

Samla alla \( x\)-termer på det led vars \( x\)-term

har större koefficient. I exemplet ovan på VL:

\(\begin{array}{rcl} 4\,x \, + \, 6 & = & 2\,x \, + \, 14 \\ \quad 4\,x \, + \, 6 \; {\color{Red} {- \; 2\,x}} & = & 2\,x \, + \, 14 \; {\color{Red} {- \; 2\,x}} \quad \\ 2\,x \, + \, 6 & = & 14 \end{array}\)

Detta för att undvika negativa \( x\)-termer.

Steg 2

Samla alla konstanta termer (utan \(x\)) på ekva-

tionens andra led. I exemplet ovan på HL:

\(\begin{array}{rcl} 2\,x \, + \, 6 & = & 14 \\ \qquad 2\,x \, + \, 6 \; {\color{Red} {- \; 6}} & = & 14 \; {\color{Red} {- \; 6}} \\ 2\,x \, & = & 8 \end{array}\)

Steg 3

Lös ekvationen enligt den allmänna metoden:

\(\begin{array}{rcl} 2 \cdot x \, & = & 8 \\ \qquad\qquad\quad \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{8}{{\color{Red} {2}}} \\ x \, & = & 4 \end{array}\)

Fall 2: \( x\)-term med större koefficient på HL

\( \qquad \)Fil:Bild Ekvation x bada sidor Fall 2 370.jpg

\( \qquad {\bf{\color{Red} 4}} \, \) är koefficienten till \( \, 4\,x \, \).

\( \qquad {\bf{\color{LimeGreen} 2}} \, \) är koefficienten till \( \, 2\,x \): \( \quad {\bf{\color{Red} 4}} \, > {\bf{\color{LimeGreen} 2}} \)

Steg 1

Samla alla \( x\)-termer på det led vars \( x\)-term

har större koefficient. I exemplet ovan på HL:

\(\begin{array}{rcl} 2\,x \, + \, 16 & = & 4\,x \, + \, 6 \\ \quad 4\,x \, + \, 6 \; {\color{Red} {- \; 2\,x}} & = & 2\,x \, + \, 14 \; {\color{Red} {- \; 2\,x}} \quad \\ 2\,x \, + \, 6 & = & 14 \end{array}\)