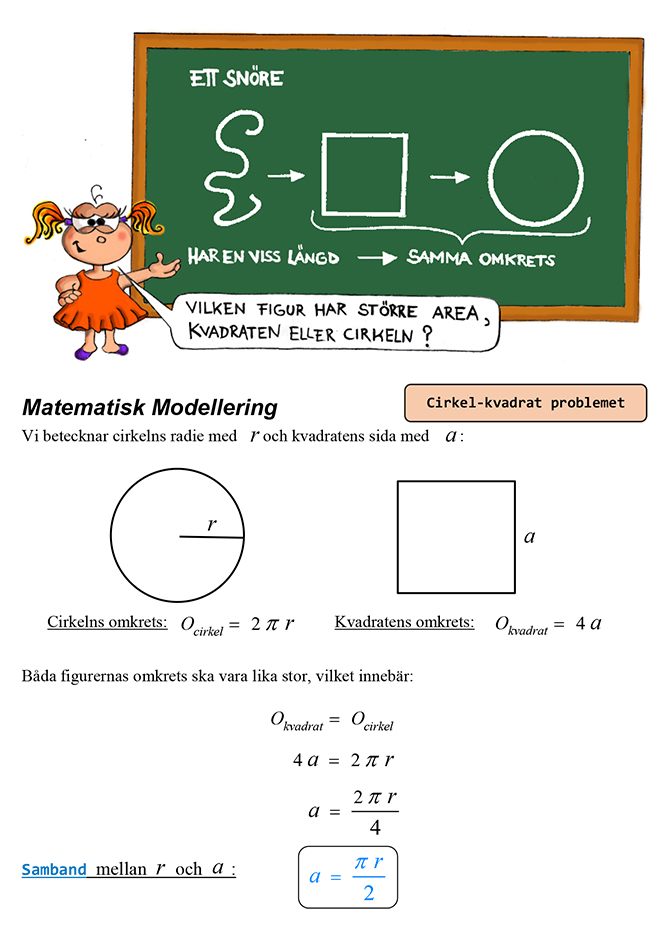
5.7 Problemlösning: Cirkel-kvadrat problemet
| <<< Förra avsnitt | Genomgång | Övningar | Det duala problemet |
Vilken figur har större area?
Slutsats
Ska cirkeln och kvadraten ha samma omkrets måste sambandet ovan gälla.
Sambandet ovan är en funktion: \( \qquad \)Dvs ett värde på \( \, r \, \) bestämmer endast ett värde på \( \, a \, \).
\( \, r \, \) är funktionens oberoende och \( \, a \, \) funktionens beroende variabel.
Dagens inlämningsuppgift
Lös Cirkel-kvadrat problemet i tre steg:
Steg 1: Ta exemplet \( \, r = 4 \, \). Beräkna \( \, a = f(4) \, \) och båda figurernas areor. Vilken är större?
Steg 2: Ta flera exempel, t.ex. \( r = 2 \), \( \; r = 6 \; \) och \( \; r = 8 \). Gör samma sak som i steg 1.
Steg 3: Lös uppgiften generellt med variablerna \( \, r \, \) och \( \, a \, \).
Fota A4-bladet med din mobil och ladda upp det till Schoolitys "Uppgift".
Deadline för inlämning: kl 18 lektionsdagen.
Dagens övningar
Gör övningarna i boken Origo 1b:
Sidan 180
I Origo 1c: Sidan 164
Kolla dina resultat i bokens facit.
Copyright © 2020 TechPages AB. All Rights Reserved.