Skillnad mellan versioner av "5.7 Problemlösning: Cirkel-kvadrat problemet"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(31 mellanliggande versioner av samma användare visas inte)
Rad 5: Rad 5:
 
{{Selected tab|[[5.7 Problemlösning: Cirkel-kvadrat problemet|Genomgång]]}}
 
{{Selected tab|[[5.7 Problemlösning: Cirkel-kvadrat problemet|Genomgång]]}}
 
{{Not selected tab|[[5.7 Övningar till Cirkel-kvadrat problemet|Övningar]]}}
 
{{Not selected tab|[[5.7 Övningar till Cirkel-kvadrat problemet|Övningar]]}}
−
{{Not selected tab|[[Det duala Cirkel-kvadrat problemet|Det duala problemet]]}}
+
{{Not selected tab|[[5.7 Lösning till Cirkel-kvadrat problemet|Lösning]]}}
 +
<!-- {{Not selected tab|[[Det duala Cirkel-kvadrat problemet|Det duala problemet]]}} -->
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
Rad 14: Rad 15:
  
 
<div class="ovnE">
 
<div class="ovnE">
 +
 +
<big>Man har ett snöre av en viss längd och vill begränsa med det en yta av maximal
 +
 +
storlek. Är det då bättre att forma snöret till en cirkel eller till en kvadrat?
 +
</big>
 +
 
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Problemlosning_1a.jpg]] </div>
 
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Problemlosning_1a.jpg]] </div>
 
</div>
 
</div>
Rad 41: Rad 48:
 
2) &nbsp; Ta flera exempel, t.ex. <math> r = 2 </math>, <math> \; r = 6 \; </math> och <math> \; r = 8 </math>. Gör samma sak som i steg 1.
 
2) &nbsp; Ta flera exempel, t.ex. <math> r = 2 </math>, <math> \; r = 6 \; </math> och <math> \; r = 8 </math>. Gör samma sak som i steg 1.
  
−
3) &nbsp; Lös uppgiften generellt med <math> \, r \, </math> och <math> \, a \, </math> som variabler. Ställ upp uttryck för figurernas areor.  
+
3) &nbsp; Lös uppgiften generellt med <math> \, r \, </math> och <math> \, a \, </math> som variabler. Ställ upp ett uttryck för arean till resp. figur.  
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Bilda förhållandet (kvoten) mellan deras areor dvs <math> \, \displaystyle \frac{A_{cirkel}}{A_{kvadrat}} \, </math>. Vilken figur har större area?
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Bilda förhållandet (kvoten) mellan deras areor dvs <math> \, \displaystyle \frac{A_{cirkel}}{A_{kvadrat}} \, </math>.  
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Räkna exakt dva bibehålla <math> \, \pi \, </math> som bokstav och använd bråk istället för decimaltal.
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Räkna <i>exakt</i> dvs bibehålla <math> \, \pi \, </math> som bokstav och använd hela tiden bråk istället för decimaltal.
 +
 
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Förenkla kvoten så långt som möjligt. Vilken figur har <i>alltid</i> större area?
  
 
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Är resultatet beroende av figurernas storlek, dvs av <math> \, r \, </math> och <math> \, a \, </math>?
 
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Är resultatet beroende av figurernas storlek, dvs av <math> \, r \, </math> och <math> \, a \, </math>?
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Ange hur många procent den ena figuren är större än den andra.
  
 
Ladda upp dina lösningar till Schoolitys "Uppgift". Deadline för inlämning: kl 18 lektionsdagen.
 
Ladda upp dina lösningar till Schoolitys "Uppgift". Deadline för inlämning: kl 18 lektionsdagen.
Rad 59: Rad 70:
 
----
 
----
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Sidan 180
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Sidorna 302-305
  
 
----
 
----
  
−
&nbsp;&nbsp;&nbsp;&nbsp;I Origo 1c:&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Sidan 164
+
&nbsp;&nbsp;&nbsp;&nbsp;I Origo 1c:&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Sidorna 290-293
  
 
----
 
----
  
−
&nbsp;&nbsp;&nbsp;&nbsp;Kolla dina resultat i bokens facit.
+
&nbsp;&nbsp;&nbsp;&nbsp;Hoppa över sånt vi inte gått genom.
 
</big></div>
 
</big></div>
  

Nuvarande version från 29 mars 2020 kl. 21.13

       <<<  Förra avsnitt          Genomgång          Övningar          Lösning      


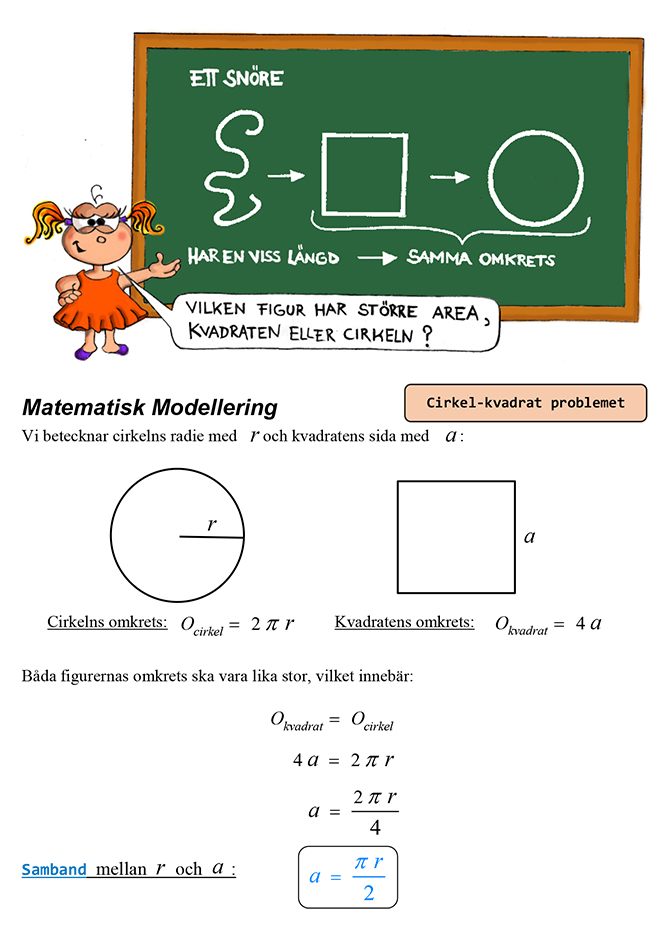
Vilken figur har större area?

Man har ett snöre av en viss längd och vill begränsa med det en yta av maximal

storlek. Är det då bättre att forma snöret till en cirkel eller till en kvadrat?

Problemlosning 1a.jpg


Slutsats

  Ska cirkeln och kvadraten ha samma omkrets måste sambandet ovan gälla.

  Sambandet ovan är en funktion: \( \qquad \)
\( \displaystyle a \, = \, f(r) \, = \, \frac{\pi}{2} \cdot \, r \)

  Dvs ett värde på \( \, r \, \) bestämmer endast ett värde på \( \, a \, \).

  \( \, r \, \) är funktionens oberoende och \( \, a \, \) funktionens beroende variabel.


Dagens inlämningsuppgift

Lös Cirkel-kvadrat problemet i tre steg:

1)   Ta exemplet \( \, r = 4 \, \). Beräkna \( \, a = f(4) \, \). Beräkna båda figurernas areor. Vilken är större?

2)   Ta flera exempel, t.ex. \( r = 2 \), \( \; r = 6 \; \) och \( \; r = 8 \). Gör samma sak som i steg 1.

3)   Lös uppgiften generellt med \( \, r \, \) och \( \, a \, \) som variabler. Ställ upp ett uttryck för arean till resp. figur.

      Bilda förhållandet (kvoten) mellan deras areor dvs \( \, \displaystyle \frac{A_{cirkel}}{A_{kvadrat}} \, \).

      Räkna exakt dvs bibehålla \( \, \pi \, \) som bokstav och använd hela tiden bråk istället för decimaltal.

      Förenkla kvoten så långt som möjligt. Vilken figur har alltid större area?

      Är resultatet beroende av figurernas storlek, dvs av \( \, r \, \) och \( \, a \, \)?

      Ange hur många procent den ena figuren är större än den andra.

Ladda upp dina lösningar till Schoolitys "Uppgift". Deadline för inlämning: kl 18 lektionsdagen.


Dagens övningar

    Gör övningarna i boken Origo 1b:

                Sidorna 302-305

    I Origo 1c:      Sidorna 290-293

    Hoppa över sånt vi inte gått genom.











Copyright © 2020 TechPages AB. All Rights Reserved.

Hämtad från "https://matte1b.mathonline.se/index.php?title=5.7_Problemlösning:_Cirkel-kvadrat_problemet&oldid=36228"