Praktisk förklaring

<-- Tillbaka till demosidan

Problemet

Teoretisk förklaring

Praktisk förklaring

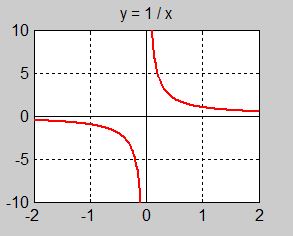
Istället för att mata in i din miniräknare \( \, 1 \, / \, 0-\) för då får du ERROR \(-\) dela \( 1\, \) inte direkt med \( 0\, \) utan med små tal.

Fortsätt med att låta dessa små tal bli mindre och mindre:

{| class="wikitable" |- ! \( x\, \) || \( {1 \over x} \) |- | align=left| \( 0,1\, \) ||align=left| \( 10\, \) |- | align=left| \( 0,01\, \) ||align=left| \( 100\, \) |- | align=left| \( 0,001\, \) ||align=left| \( 1000\, \) |- | align=left| \( 0,000\,1 \) ||align=left| \( 10\,000 \) |- | align=left| \( 0,000\,01 \) ||align=left| \( 100\,000 \) |- | align=left| \( 0,000\,001 \) ||align=left| \( 1\,000\,000 \) |- | align=left| \( 0,000\,000\,1 \) ||align=left| \( 10\,000\,000 \) |- | align=left| \( 0,000\,000\,01 \) ||align=left| \( 100\,000\,000 \) |- | align=center| \( \cdots \) ||align=center| \( \cdots \) |- | align=center| \( \rightarrow 0 \) ||align=center| \( \rightarrow \infty \) |}

\( \qquad \)

Experimentet visar: Ju mindre \( x\, \) blir desto större blir \( {1 \over x} \). I gränsfallet \( x = 0\, \) blir \( {1 \over x} \) oändligt stort.

\( \infty \) är symbolen för oändligheten. Det är omöjligt att ange \( \infty \). Vad man än anger så kan man alltid lägga \( \, 1 \, \) till det och få ett tal som är större. Så kan man hålla på i evighet.

Därför är \( \infty \) inte något tal som man kan räkna med. Man säger:

\( {1 \over x} \) går mot oändligheten utan att nå den någonsin, när \( \, x\, \) går mot \( \, 0\, \).

Slutsats: \( {\color{White} x} {1 \over 0} \) är inget tal och därför inte definierat.