Praktisk förklaring
| <-- Tillbaka till Matte 1b:s starsida | Problemet | Teoretisk förklaring | Praktisk förklaring | Vad händer om ... ? |
Istället för att mata in i din miniräknare \( \, 1 \, / \, 0-\) för då får du ERROR \(-\) dela \( 1\, \) inte direkt med \( 0\, \) utan med små tal.
Mata in i din miniräknare:
- \[ 1 \, / \, 0,1 \qquad 1 \, / \, 0,01 \qquad 1 \, / \, 0,001 \qquad \ldots \]
Fortsätt med att låta de små tal som du delar med, bli mindre och mindre, se tabellen.
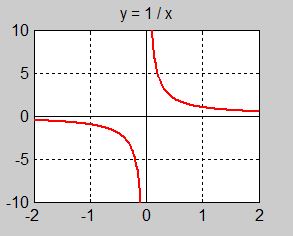
Eller rita grafen \( \, y \, = \, 1/x \, \) och titta på \( \, x \rightarrow 0 \,\).
Både tabellen och grafen: Ju mindre \( \, x \, \) blir desto större blir \( \, 1/x \, \). I gränsfallet \( \, x=0 \, \) blir \( \, 1/x \, \) oändligt stort.
Man säger: \( \displaystyle {1 \over x} \) går mot oändligheten när \( \, x\, \) går mot \( \, 0\, \) och skriver: \( \, \displaystyle {1 \over x} \to \infty \, \) när \( \, x \, \to \, 0 \).
\( \infty \) är symbolen för oändligheten. Det är omöjligt att ange \( \infty \) som ett tal som man kan räkna med.
Vilket tal man än anger så kan man alltid göra \( \, + \, 1 \, \) och få ett större tal. Det tar aldrig slut.
Slutsatser: \( \displaystyle \quad {1 \over 0} \) är inget tal och därmed inte definierat.
Slutsatser: \( \quad \)Det är matematiskt inte korrekt att skriva \( \displaystyle \, {1 \over 0} = \infty \, \). Korrekt: \( \displaystyle \, {1 \over x} \, \to \, \infty \, \) när \( \, x \, \to \, 0 \).
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.